2019-09-30 (Mon)
本日のキーワード : 有理数、無理数
有理数(ゆうりすう、英: rational number) とは、二つの整数 a, b (ただし b は 0 でない)をもちいて a/b という分数で表せる数のことをいう。b = 1 とすることにより、任意の整数は有理数として扱うことができる。
無理数(むりすう、 英: irrational number)とは、有理数ではない実数、つまり分子・分母ともに整数である分数(比 = 英: ratio)として表すことのできない実数を指す。実数は非可算個で有理数は可算個であるから、ほとんど全ての実数は無理数である。
本日の書物 : 『素数はなぜ人を惹きつけるのか』 竹内薫 朝日新聞出版
戦後の日本人は、正しい歴史を学校で教わって来ませんでした。
そして、現代のメディアもまた、嘘の情報を流し続けています。
私たち日本人は、親日的な立場に立ち、正しく認識し直し、
客観的に情勢を判断する必要があります。
それでは、この書物を見ていきましょう!
『 先に、自然数は物を数えるときの数であり、それには偶数と奇数があり、さらに【奇数】のうちに【素数】があるという話をしました。
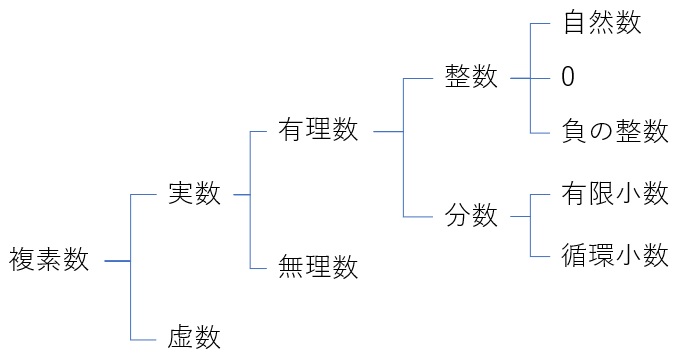
しかし、われわれは、そのほかに0やマイナス、分数、それから小数も使います。これらの数は一体どのように整理されるのでしょうか?これらの数は、自然数と違ってたしかに子どもには理解しにくい、"不自然"な側面があるのかもしれません。…
たとえば、3分の2という【分数】を理解するには、自然数である2と3の【「比」】であるという【概念】を持つことが必要です。比は「比べる」という意味。つまり、2:3というふうに2と3の大きさを比べるんです。一方【小数】は、0・666666…という具合に、3分の2の【割り算を実行した数】のことです(ためしに2÷3を計算してみてください)。
さらに【分数と小数の関係】も【重要】です。【小数であらわすことができる数】は、実は【2種類】あり、一つは【分数の形に変換できる数】、もう一つは【分数にはできない数】です。…

【分数の形にできる】ということは、ようするに、…【比の形で書きあらわすことができる】ということです。そこで、この数を【「比が有る数」】、つまり【有比数】と呼ぶことができるでしょう。この言葉に聞き馴染みのない方もいるでしょうが、それはあたりまえ。なぜならば、この有比数という言葉は"竹内語"だからです。学校では、【「有理数」】と教わります。
有比数は英語で【rational number】といいますが、このrationalとはどのような意味でしょうか。辞書を引くと一番初めに「合理的な」とありますが、実はもう一つ【「比の形にできる」】という意味があるのです。本来は、この後者の意味であるはずなのに、rational numberを日本語に訳すときに、「合理的な」の方を採用してしまったのです。ちょっと誤訳っぽいですよね。
学校では「有理数」の他に「無理数」というものを教わります。【「無理数」】とは、【比の形にあらわすことができない小数点以下が無限に続いている数】なので、竹内語では【「無比数」】!
この無比数の歴史は古く、古代ギリシャのピタゴラスが、正方形の対角線と辺の長さが整数の比にならないことに気づいていたともいわれます。あるいは円の直径と円周の関係(円周率π)も整数ではありませんね。正方形や円のような幾何学の基本的な図形にすら無比数が潜んでいるのです。
ところが小数点以下が無限に続いていても、例外的に比の形にあらわすことができる場合もあります。たとえば0・333333…と3が永遠に続く数字(【循環小数】)は、3分の1です。ウソだと思うなら、1を3で割ってご覧なさい。永遠に計算が終わらないでしょう。このように、小数点以下が無限に続く終わりがない数でも有比数になることがあるんです。
小数点以下の数が無限に続いている数が【有比数なのか無比数なのか】を知りたい!そんなときには、【「繰り返しのパターン」があるかどうかで判別】することができます。たとえば0・321321…という具合に「321」の繰り返しがあるような場合は、必ず有比数です。
それに対して繰り返しのパターンが出てこない場合は無比数です。』

「+×タイプ」と「×+タイプ」を繋いだら、「++タイプ」になる!
いかがでしょうか?
今回ご紹介させていただく書物は、「素数」について、数学や物理学のお話を中心に分かりやすく解説がなされていて、その流れの中で、いくつもの公式が登場してくるのですが、特徴的なのが、その数式は「観賞用」として載せられている点で、「数式そのものを楽しむ」という視点で書かれていて、数学が苦手な方でも十分に楽しんで頂ける良書となります。

さて、本日は早速本題に入らせて頂きたいと思いますが、ポール・クルーグマンの論文を読み進めていくうちに、次のような何だか意味不明な数式が登場してきました。

『 財が一つで、representative agent 経済(ただし、エージェントはそれぞれ自分の消費分は他人から買わなきゃいけない)を考える。はじめは、財が非弾性的に供給されるものとしよう。つまりそれぞれのエージェントが一定のほどこし yt を毎期ごとにもらえるものとしよう。具体性をつけるため、効用関数は以下のような形を取るものとする。』
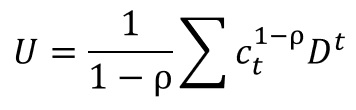

この数式が何を意味しているのかが理解できない方にとっては、ここから先へと進むことができないのではないかと思い、少々お話から脱線させて頂いているところとなります。
何故ならば、この数式が理解できないのは、そもそも、書かれている数式が一体何を表現していて、それがどのように振舞うのかがイメージできないからでは?と当ブログでは考えています。
そこで、いま、函数(関数)というものについて、「足し算」と「掛け算」からなる4つのパターンに分類して、それらの数式が意味しているものをイメージできるようになるために、少しずつ書かせて頂いているところです。
つまり、昨日のところでも、「方程式」と「函数(関数)」の違いについて書かせて頂きましたが、「方程式」を解くのではなく、まずは「函数(関数)」がどのように振舞うのかを確認しているところということになります。
一昨日のところまで(→「消費税増税」と「お・つ・む・な・し」)に、2つの異なったパターンの「函数(関数)」を、“勝手に想像”して、それがどのように振舞うのかを考えました。
《 「++タイプ」 : 足し算を足し算にする函数(関数) 》
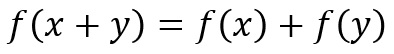
という形をした、足し算を足し算にしている函数(関数)を、「++タイプ」と名付け、それが「どのように振舞うのか」を考えてみますと、cを定数とした場合に、
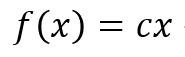
という“直線の形”をしている、ということが判明しました(→消費税増税の実施はあくまでもその時点での経済状況の判断に依存するもの、なはずなのですが。。。)。
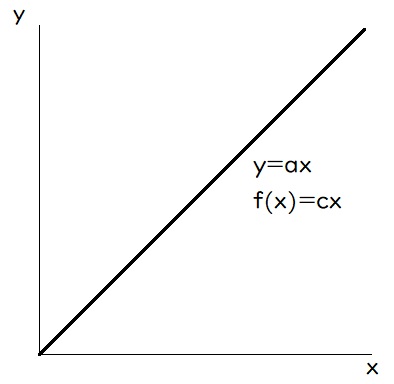
《 「+×タイプ」 : 足し算を掛け算にする函数(関数) 》
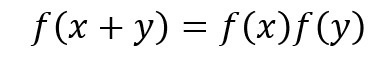
という形をした、足し算を掛け算にしている函数(関数)を、「+×タイプ」と名付け、それが「どのように振舞うのか」を考えてみますと、cを定数とした場合に、
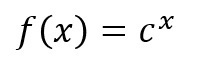
となり、この函数(関数)は、「c」が正の数(つまり、「c>0」)かつ「1ではない」(c≠1)、次のような“曲線の形”をしています。これを一般に、「指数関数」と呼びます。
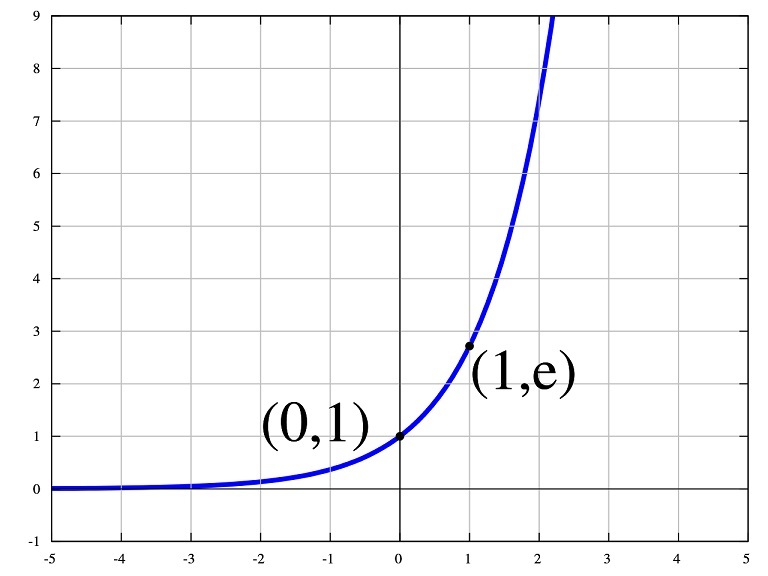
そして、未だに何か良く分かっていないものとして、ある一つの特別な函数(関数)「E」があって、それは以下の条件を満たすものなのですが、
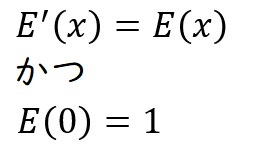
この微分しても(導関数を求めても)、自分自身の導関数と等しくなる(=微分しても変わらない)、特別な唯一の函数(関数)を成り立たせるための、特別な数、それを「e」と表しますと、次のように表現することができます。
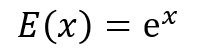
しかし、この「e」の正体が何なのかは、現時点では知りません。

それでは、本日からは3つ目のパターンとして、次のような函数(関数)を、またまた“勝手に想像”(混乱を避けるために、今回は「f」ではなく「g」を用いています)して、
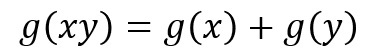
掛け算を足し算にしているので、「×+タイプ」と名付け、それが「どのように振舞うのか」を考えてみたいと思います。
それでは参ります💗
いま、「+×タイプ」を「f」、「×+タイプ」を「g」とした場合、
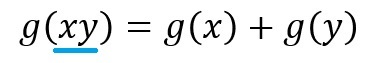
「×+タイプ」の「g」の函数(関数)、つまり、ただ単なるハコ(函、箱)に過ぎない、まるで自動販売機のような装置に、「xy」(x掛けるy)という何か分からないものを投入すると、それが「どのように振舞うのか」を考えてみようとしているわけですが、「+×タイプ」の「f」については分かっていますので、
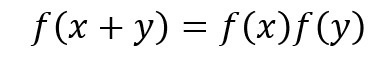
「xy」(x掛けるy)の部分が「+×タイプ」(ならばこうなる→f(x+y)→f(x)・f(y))として、それを投入してみますと、
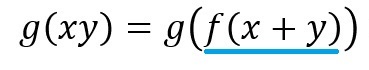
となり、
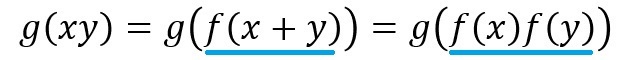
となることが理解できます。
で、「×+タイプ」は、
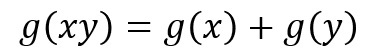
と定義しました(=“勝手に決めた”)ので、
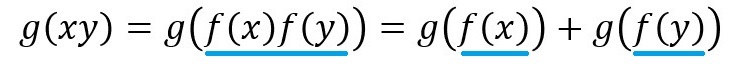
つまり、
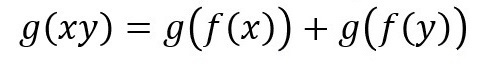
となります。いまやったことは、「+×タイプ」の「f」の出力部分と、「×+タイプ」の「g」の入力部分を繋いだだけ(↓その一連の流れ)ですが、下線部分にご注目して頂き、
新たに「h」を用いて、
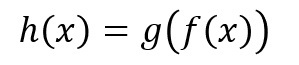
と表現いたしますと、
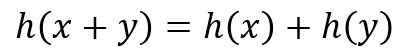
となりますので、これは、一番最初に試みた「++タイプ」のパターンであることが理解できます。
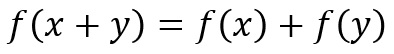
「+×タイプ」と「×+タイプ」を繋いだら、「++タイプ」になっちゃった、という不思議な現象が起こっていますが、本日はここまでとさせて頂きます。

続きは次回に♥
ランキング参加中で~す^^ ポチっとお願いします♥
↓↓↓↓↓↓↓
にほんブログ村

人気ブログランキング


- 関連記事
-
- 比例と反比例の違いが分からない人が多くいるのですが・・・ (2019/10/07)
- 安倍政権の「社会主義政策」と「算数」すら理解できない全野党 ~ 国会議員は「おバカ」しかいない? (2019/10/06)
- 1から順に無限まで足していったら・・・いくつになるの? (2019/10/05)
- 宇宙の数学的な整合性 ~ 「超ひも理論」 (2019/10/04)
- 安倍政権の「社会主義政策」 ~ 操られる「パヨク」&踊らされる「ネトウヨ」、という「お馬鹿」の極みwww (2019/10/03)
- 円周率の「π(パイ)」と素数に関する函数(関数)の「π(パイ)」 (2019/10/02)
- 函数(関数)の眺め方 (2019/10/01)
- 「分数にできる数」と「分数にできない数」は、どっちが多いの? (2019/09/30)
- 「函数(関数)」と「方程式」と「恒等式」の違いって何? (2019/09/29)
- 「ゼロ金利」と「マイナス金利」と「虚数金利」 (2019/09/21)
- 「作ったモノが必ず売れる」という世界 ~ 古典派経済学の必要十分条件 (2019/09/19)
- 財務省と日銀とマルクス経済学 (2019/09/18)
- 消費増税すれば、どうなる? 数学の論理を駆使する要(かなめ) ~ 「必要条件」と「十分条件」 (2019/09/17)
- 「目で見えるものだけが全てではない」ということが理解できない「お馬鹿」 (2019/09/12)
- 実は、コッソリとやっている、「アベノミクス」から「アベ・デフレノミクス」への政策変更 (2019/09/11)
