安倍政権の「社会主義政策」　～　操られる「パヨク」＆踊らされる「ネトウヨ」、という「お馬鹿」の極みｗｗｗ

2019-10-03 (Thu)

$math-banner.jpg$

本日のキーワード　：　多項式

数学において、多項式（たこうしき、英: polynomial）、または整式（せいしき）とは、数と不定元（変数とも呼ばれる）をもとにして、和と積によってつくられる式のことである。

本日の書物　：　『素数はなぜ人を惹きつけるのか』　竹内薫　朝日新聞出版

戦後の日本人は、正しい歴史を学校で教わって来ませんでした。

そして、現代のメディアもまた、嘘の情報を流し続けています。

私たち日本人は、親日的な立場に立ち、正しく認識し直し、

客観的に情勢を判断する必要があります。

それでは、この書物を見ていきましょう！

『　前章で【ガウス】が発見した【素数公式】をご紹介しました。

カール・フリードリヒ・ガウス

思い出してみてください。こんな恰好をしていましたよね？

《　ガウスの素数公式①　》

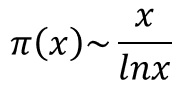
　実はこの素数公式、ガウス自身がもう少し精度の高い式を発見しています。それは、こんな形をしています。

《　ガウスの素数公式②　》

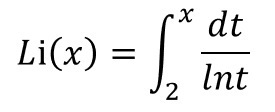
　あわわ、なにコレ～、この本、一般向けじゃなかったの～？

　【積分】が出てくるなんて聞いてないよ～。

　まあまあまあ、どうか慌てないでください。無問題（ノープロブレム）ですから。

たしかにこの２番目の素数公式は積分記号になっていますが、そもそも【積分というのは「足し算」と同じ発想】。【細かく切り刻んで足すことを積分という】のです。

なので、xが大きな数の場合、同じ式を次のように書いてもかまわないんです。

《　ガウスの素数公式②´　》

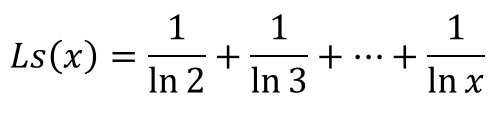
　ええと、素数公式②が意味することの「ぶっちゃけた説明」が素数公式②´だと考えてくださいね。足し算にしてしまえば、さほど難しく感じないはずです。

　そうそう、ついでに記号の説明もしておきましょう。【LiのLは「対数の」（logarithmic）の頭文字】で、【Liのiは「積分」（integral）の頭文字】。同様に、【Lsのsは「和」（sum）の頭文字】になっています。こうやって記号の由来を突き詰めてゆくと、数式もそんなに怖くなくなるから不思議です。

　ここで読者のみなさんに覚えておいていただきたいのは、【素数公式にも、いろんなバージョンがある】ということ。ガウスの素数公式もバージョン①から②´まであるわけです。』

日本国民の「財産を収奪」する安倍政権の社会主義政策

いかがでしょうか？

今回ご紹介させていただく書物は、「素数」について、数学や物理学のお話を中心に分かりやすく解説がなされていて、その流れの中で、いくつもの公式が登場してくるのですが、特徴的なのが、その数式は「観賞用」として載せられている点で、「数式そのものを楽しむ」という視点で書かれていて、数学が苦手な方でも十分に楽しんで頂ける良書となります。

さて、昨日のところでは、ここ最近、一体何をやっているのか「迷子」にならないようにするために、「アレコレ」と考えてきた函数（関数）の振舞いについて、これまでの流れを再確認しました。

で、そもそも、どうして、こんな面倒なことをやっているのかと申しますと、「安倍政権」と「与党自民党＋世界公認のカルト集団・公明党」がマルクス主義者の“革新官僚”であった岸信介のごとく、「社会主義政策に舵を切った」ことに、大多数の日本国民が気が付かないまま、それぞれの「財産を収奪される」ことになったため、みなさま御自身のアタマで、その是非を考えられるように、微力ながら貢献させて頂きたいと考えているからです。

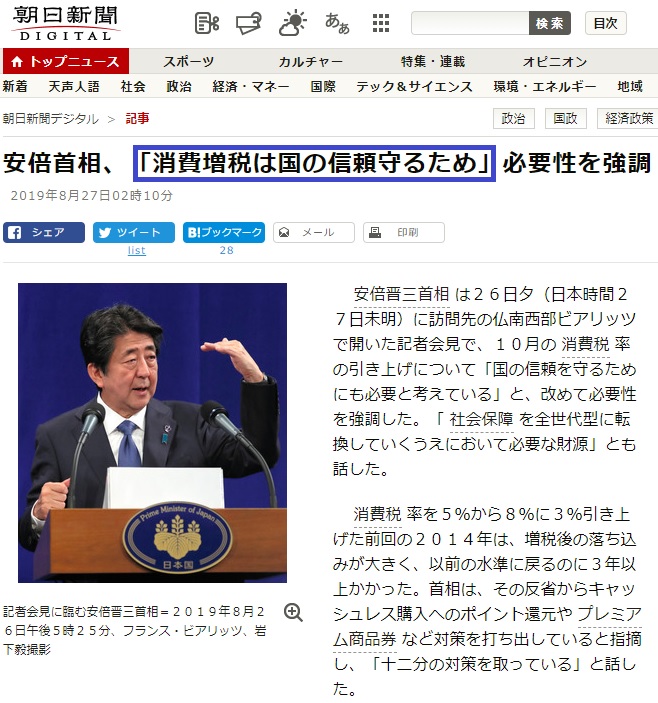
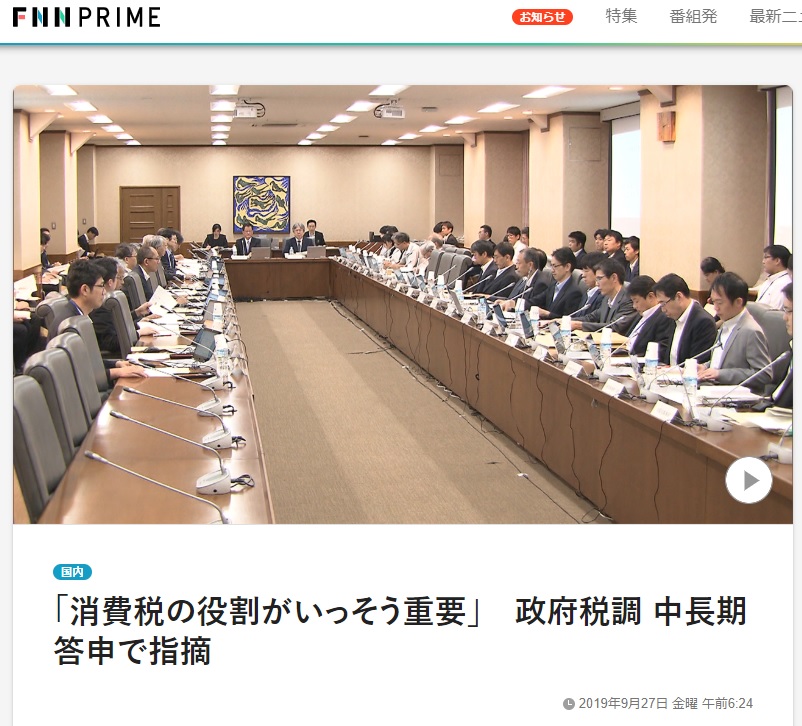
☆「消費税の役割がいっそう重要」　政府税調中長期答申で指摘 - FNNプライムオンライン

その背後にいる「害虫」が、財務省の“小物官僚ども”です💗

しかも、何の役にも立たない、東京大学（あ）法学部を卒業した“だけ”の“無知で幼稚な学士”たちが、自分たちの、その無能ぶりを“糊塗するため”に、私たち日本国民の生活を犠牲にしようとしているわけです。

ですよね？　おかもっちゃんｗｗｗ

岡本薫明（おかもとしげあき）

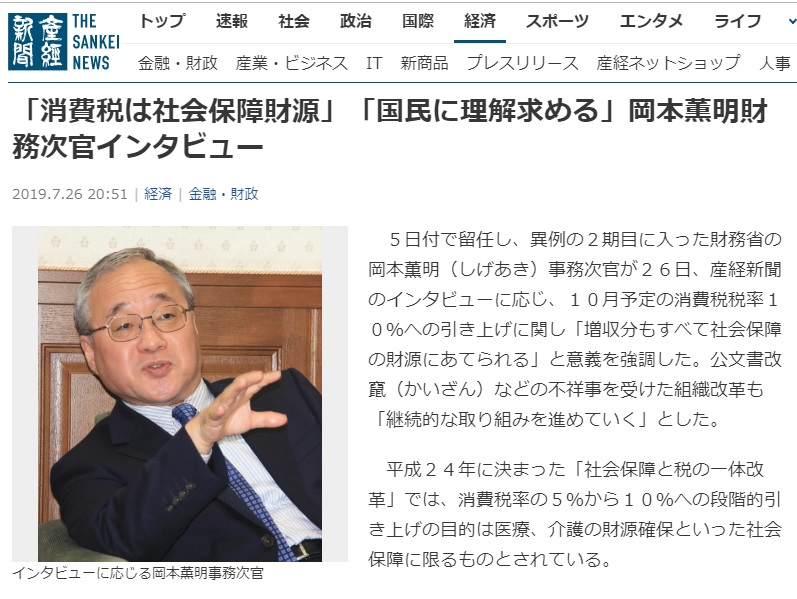
☆「消費税は社会保障財源」「国民に理解求める」岡本薫明財務次官インタビュー

安倍政権が「社会主義政策に舵を切った」ということは、簡単に申し上げますと、「日本をぶっ壊す！」ということです💗　つまり、「左翼リベラル（パヨク）」と瓜二つ、あの「悪夢の民主党政権」と同一と言っても過言ではありません（もっとも、自民党以外のすべての野党も、それ以上に無能極まりないのですがｗ）。

それが証拠に、今回の安倍政権による「勝手な消費税増税」は、まともな経済学者（つまり、御用学者ではない専門家）からは、集中的に批判されています💗

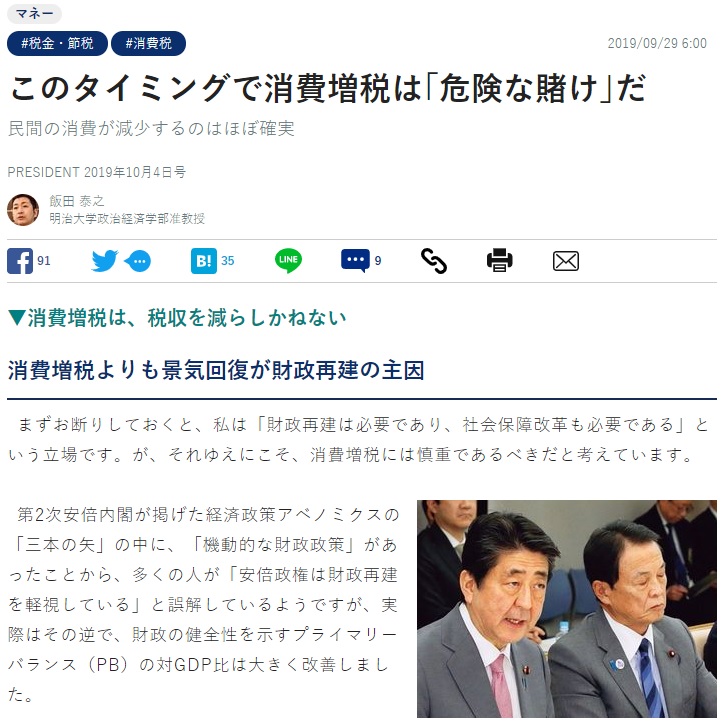
☆このタイミングで消費増税は｢危険な賭け｣だ民間の消費が減少するのはほぼ確実 #POL

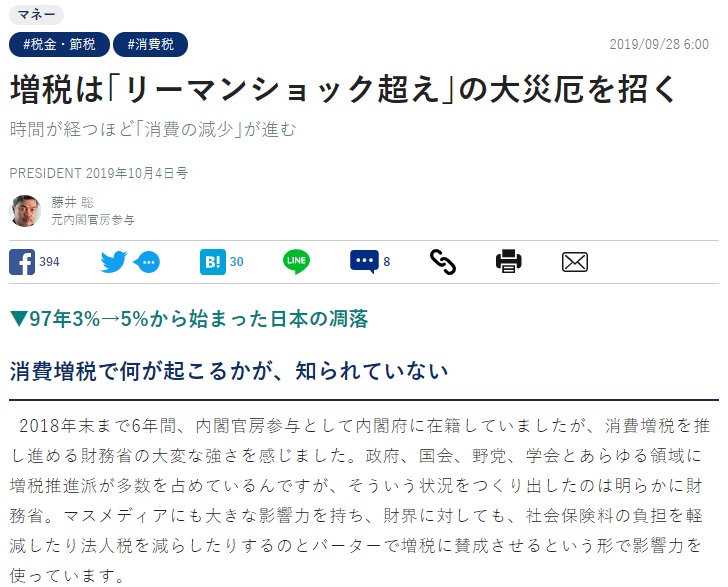
☆増税は｢リーマンショック超え｣の大災厄を招く時間が経つほど｢消費の減少｣が進む #POL

そして、同じようなことが、実は２０年以上も前にも起こっていて、それこそが、私たち日本国民が知っておくべきは、ポール・クルーグマンが２０年以上も前に、我が国の惨状を見て、提唱した理論になります。

ポール・クルーグマン

詳しくはこちらをご参照💗
↓
☆２０年以上前の失敗から何一つ学べない財務省・日銀　～　「緊縮財政」と「消費税増税」

☆「It's Baaack：Japan's Slump and the Return of the Liquidity Trap」By Paul R.KRUGMAN

　

そこで、ポール・クルーグマンが、何をせよとアドバイスしているのかを、山形浩生氏の訳による「復活だぁっ！　日本の不況と流動性トラップの逆襲」から確認していたところ、

☆「復活だぁっ！　日本の不況と流動性トラップの逆襲」山形浩生訳　

論文を読み進めてゆくと、何だか意味不明な数式が登場してきました。

『　財が一つで、representative agent 経済（ただし、エージェントはそれぞれ自分の消費分は他人から買わなきゃいけない）を考える。はじめは、財が非弾性的に供給されるものとしよう。つまりそれぞれのエージェントが一定のほどこし yt を毎期ごとにもらえるものとしよう。具体性をつけるため、効用関数は以下のような形を取るものとする。』

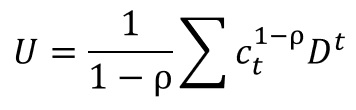
この数式が何を意味しているのかが理解できない方にとっては、ここから先へと進むことができないのではないかと思い、少々お話から脱線させて頂いているところとなります。

何故ならば、この数式が理解できないのは、そもそも、書かれている数式が一体何を表現していて、それがどのように振舞うのかがイメージできないからでは？と当ブログでは考えているからです。

本文中にも登場していましたが、

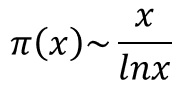
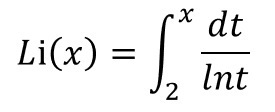
だとか、

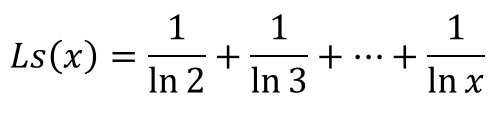
だとかって、一体、何を言っているのでしょうか？

まずは、「急がば回れ」。

「匍匐前進（ほふくぜんしん）」で！

昨日までに、函数（関数）というものについて、「足し算」と「掛け算」からなる４つのパターンに分類して、「＋＋タイプ」、「＋×タイプ」、「×＋タイプ」の３つの函数（関数）が、それぞれどのように振舞うのかについて確認してきました。

しかし、何か良く分からない特別な数「e」というものが存在しているようなんです。

そこで、最後に残る「××タイプ」の函数（関数）を考える前に、チョコっと寄り道をさせて頂きたいと思います。

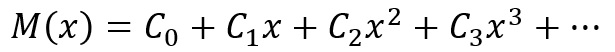
上の函数（関数）「M（x）」は、何らかの数「c」（添え字は、それぞれの「c」が別々であることを区別するために付けています）と、そこに掛け算される「x」からなる「足し算」と「掛け算」で表される函数（関数）になります。これは、学校のお勉強で「多項式」という名前で呼ばれているものになります。

この「M（x）」という函数（関数）の右辺は、御覧のように、「・・・」と無限に続くのですが、次回以降に、この何だかよく分からない函数（関数）を、もっと簡単に分かるような形に変形させて、その正体を暴いてしまおう！って考えています。

さて、どのようにすれば良いのでしょうか？