親子チョコ💗(５００冊以上の良質な書籍のご紹介)

本日のキーワード　：　応用

本日の書物　：　『とんでもなく役に立つ数学』　西成活裕　KADOKAWA/角川学芸出版

『　それでは、【数学とは何か】という中身の話に入りましょう。数学では【「公式」という言葉】がよく出てくるよね。「公式に当てはめて」っていうやつ。これはね、一言でいうと【論理】なんです。「AであればB→BであればC→CであればD」というのは論理だよね。たとえば「お腹がすいたからご飯を食べる」「睡眠不足で眠い」、こういうのも一種の論理だと考えることができます。



　私はたまにテレビに呼ばれると、ディレクターから「先生、番組で発言するときは、１段で説明してください」と言われたりします。これはどういうことかというと、「AであればB」で終わってください、ということです。

　大学の先生というのは話が下手なので、「AだからB、だからC、よってDではなくEだ」ってしゃべるわけ。かなり集中して聞かないとわからなくなる。それに話が長い人って、聞いていて疲れるよね。校長先生とか、長いでしょう(笑)。

　でも、「AだからBだ」の１段で終わる説明は、ほとんど何も考えていなくてもわかっちゃう。私はいつもテレビでも【２段ぐらい入れる】んだけれど、そうすると【必ずカットされてしまう】んですね。



　「AだからB」の段数が増えていくと、だんだん複雑になってわからなくなりますが、さて、みなさんはこれを何段ぐらい耐えられますか？ 実は、【数学ができる人】というのは【これが１万段ぐらい耐えられる】。【１０万段ぐらいいける人もいます】。そして、その一個一個を非常に正確にトントントンとのぼっていけるのです。何段で結論にたどりつけるか、この手順が大事。【将棋でも同じ】。』

数学を使って問題を解くという実例①

いかがでしょうか？

今回ご紹介させていただく書物は、高校生を対象として、実際に著者が４コマの授業を行った、そのやりとりがまとめられた書物で、対話形式で非常に読みやすく、「数学」がどのように社会の役に立っているのかを具体的に知ることができる良書となります。



さて、本書の中で、次のような問題が高校生の子どもたちに出題されます。

まず、２点間を結ぶ最短距離は、次のような直線になりますが、



一辺が１０cmの正方形の４つの角（かど）に、次のように４つの点が配置されている場合、それらを繋ぐ最も短くなる線を引いてください、というものになります。



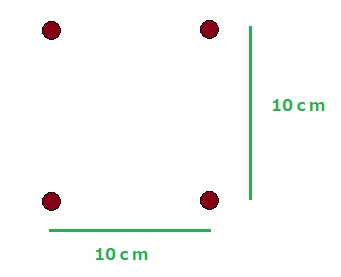
そして、高校生の子どもたちは、最初に次のような推測をします。



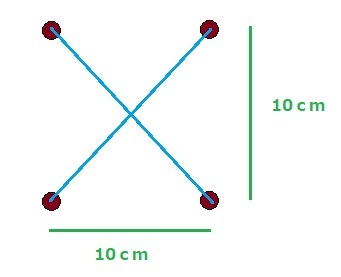
でも、正解は、これよりも、もっと短くなるパターンがある、というものでした。

その答えは載せられているのですが、解き方は書かれていなくて、高校３年生で習う微分・積分で計算ができるようになると説明されています。



それでは、早速、解いてしまいましょう💗　といっても、まだまだ、当ブログでは「微分積分学」を発明するまでには至っていないのですが、これまでにやって来たことだけで、簡単に解くことができます。



それでは、まず、さきほどの対角線で繋げた場合の、下図で示す青い線分の合計の長さを計算します。

これは簡単で、三平方の定理（ピタゴラスの定理）を理解していれば、答えは出ます（→テレビを観ることと「学歴」は関係するの？）



一辺の長さが１０cmの正方形でしたので、その対角線の長さの和は、



となります。で、正解は、これよりも短くなるのですが、どのように考えれば良いのでしょうか？



最初から、答えが分かるはずもありませんので、アレコレと考えながら進めるしか方法はないのですが、例えば、下図に示すような赤い線で繋げた場合、どうなるでしょうか？



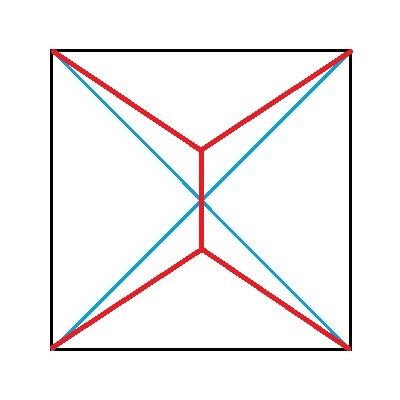
それでは、参ります！　分かりやすくするために、次のように補助線を引いておいて、

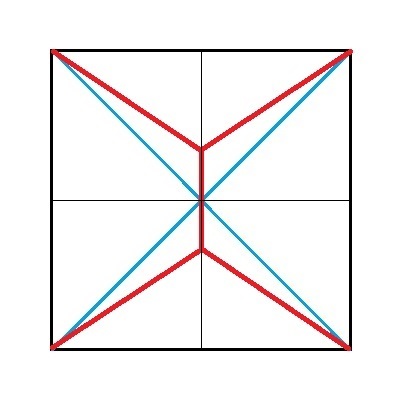
左下の小さな正方形の部分に着目します。


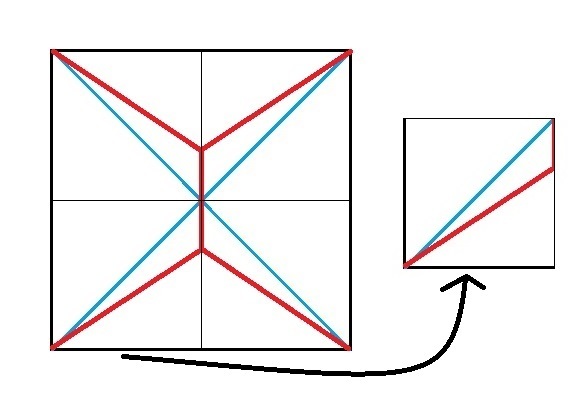
そして、ここで、その小さな正方形の中の赤い垂直な線分の長さを「x」、斜めの線分の長さを「y」と致しますと、

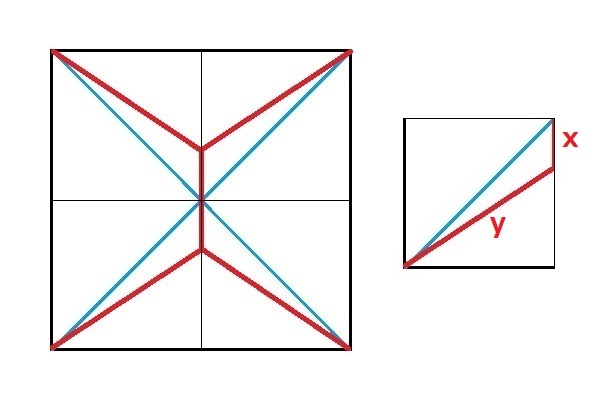
求めたい大きな正方形の中の赤い線分の長さの合計は、



であることになります。ですので、この数値が、さきほどの「２８．２８cm」よりも短い、最短となる場合を考えれば良いということになります。



で、さきほど着目した小さな正方形の部分を、右に９０度、コテンと回転させると、次のようになりますが、「x」が増加するに従って、「y」が減少していく、というイメージをアタマの中で描いてみて下さい。



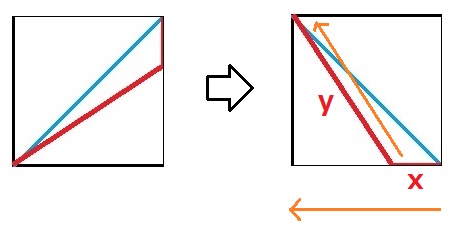
そう致しますと、これは「三角法」が使えることに気付かれると思います。







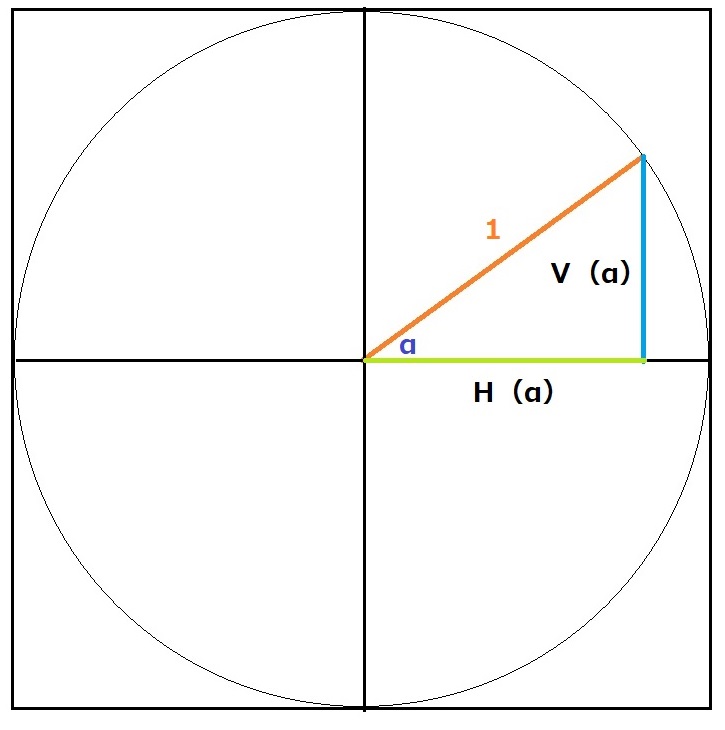
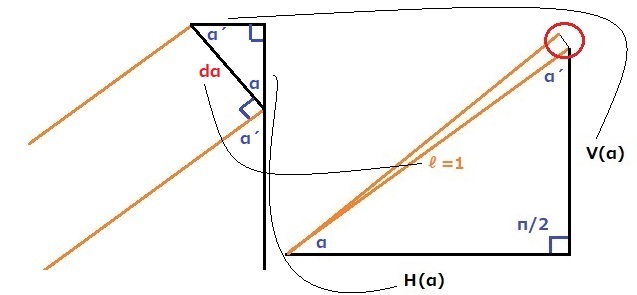
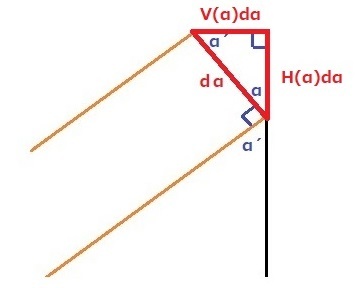
さて、どのように進めていけば良いのでしょうか？




続きは次回に♥

関連記事

• 消費増税すれば、どうなる？　　数学の論理を駆使する要（かなめ）　～　「必要条件」と「十分条件」 (2019/09/17)
• 「目で見えるものだけが全てではない」ということが理解できない「お馬鹿」 (2019/09/12)
• 実は、コッソリとやっている、「アベノミクス」から「アベ・デフレノミクス」への政策変更 (2019/09/11)
• 今は２００年に一度しかおこらない太陽のめずらしい姿を見ることができる貴重な時期なんです (2019/08/18)
• 太陽の明るさ　～　太陽が元気なときも、そうでないときも、ほとんど変わらない (2019/08/17)
• 太陽が原因で、地球で停電が起こるわけ (2019/08/16)
• 数学を勉強しても、それを実際に使えないと、まったく意味がありません (2019/04/18)
• 「数学」のテストの問題を解くということと、「数学」を実際に用いて問題を解くということの違い (2019/04/17)
• 多くの職業や社会的な地位で成功するための必須の精神力 (2019/02/22)
• フランスの「黄色」、アメリカの「緑色」、日本の「青色」 (2019/02/20)
• 「算数アタマ」のままなヒト、「数学アタマ」になれた人 (2019/02/19)
• 憲法違反の「外国人参政権」を推進するという、とっても、おバカな立憲民主党の考え方 (2019/02/18)
• 立憲民主党の「外道の政治」 (2019/02/15)
• 金融機関と文系アタマ (2019/02/14)
• ネットの「後追い」をする、とても恥ずかしい日本のメディア (2019/02/13)