2019-12-01 (Sun)

本日のキーワード : 内閣法制局、国賊
国賊(こくぞく) : その国民でありながら国家に害ある者。
本日の書物 : 『13歳からの「くにまもり」』 倉山 満 扶桑社
戦後の日本人は、正しい歴史を学校で教わって来ませんでした。
そして、現代のメディアもまた、嘘の情報を流し続けています。
私たち日本人は、親日的な立場に立ち、正しく認識し直し、
客観的に情勢を判断する必要があります。
それでは、この書物を見ていきましょう!
『 このように、【現在の日本は法制局と主計局が支配する官僚国家】です。これは【政治家を甘やかし続けた日本国民の責任】です。そして支配者である【官僚の増長は甚だしく】、とうとう【皇室にまで手をかけてきました】。

最近、【内閣法制局の力がはっきり示された例】があります。【平成から令和へと元号が変わった時のことです】。
今の上皇陛下がご譲位されることが決まって、【新帝陛下の元号を準備】することになった時のことです。手続きに時間がかかることを理由に、新帝陛下が【皇位を引き継ぐ践祚(せんそ)の前】に【新元号を発表】してしまおうという【暴挙が行われました】。

新帝陛下の皇位継承は令和元(2019)年五月一日、新元号の公表は先立つ四月一日、年度の変わり目です。 …
では、【元号を新帝践祚前に発表したのは、何だったのでしょうか】。
【元号法】には、【「天皇の代替わりがあった時にだけ変える」】とだけ書いてあります。
昭和五十四年法律第四十三号
元号法
1 元号は、政令で定める。
2 元号は、皇位の継承があつた場合に限り改める。
附 則
1 この法律は、公布の日から施行する。
2 昭和の元号は、本則第一項の規定に基づき定められたものとする。
ところが【内閣法制局】は、【「事前公表しただけだから、変えたわけではない」と主張】します。だから、お役所の文書である公文書では「絶対に令和を使うな」とお達しを出したのです。…
今回、【史上初めて元号の事前公表が行われました】。

政府は「【ウィンドウズのシステム対応が大変】だ。だから事前公表しなければならない」との説明で押し切りました。しかし、【マイクロソフト社は即座に否定】しています。また、【日本中のシステムエンジニアから笑い者にされました】が、【システム対応に1か月もかかるなど、ありえない】のです。
では、【なぜ政府は事前公表にこだわったのでしょうか】。いまだに公式見解は、「ウィンドウズのシステム対応が大変だと思った」です。いかに子供じみていても、公式見解をいくらつついても、【それ以上の本音は出てこない】でしょう。そこで、事実と論理で突き詰めていくしかありません。
そこで【考える手掛かり】となるのが【歴史】です。』

内閣法制局が皇室に対してやったこと
いかがでしょうか?
今回ご紹介させていただく書物は、タイトルにもありますように、中学生からでも十分に理解できるように書かれた、リーダーの中のリーダーが学ぶ『帝王学』を教えて下さる良書で、もしも、自分が総理大臣であったら、この国のために、何をどのようにしていくべきなのか、それを自分で考えることができるようになるための書物になります。本書をご覧頂き、一人でも多くの有志が、世の中で活躍されるようになれば、と当ブログでは考えています。

さて、本書のご紹介は本日で最後となるのですが、今回の改元の何が問題であったのかが、お判りでしょうか? 詳しくは、ぜひ、本書をご覧頂きたいのですが、一つは、「史上初めて元号の事前公表」と書かれていたように、「先例」を破ったこと、そして、もう一つが、「天皇陛下の権限」を奪ったこと、です。つまり、「内閣法制局」の小物官僚どもは、「皇室を足蹴にした国賊」ということになります。

また、本文中に、元号法の“解釈”において、内閣法制局が、「事前公表しただけだから、変えたわけではない」と主張したとも書かれていましたが、「法律の論理」のエッセンスが理解できれば、この「解釈」というものが「嘘である」ということがハッキリと判るようになります。
「法律の論理」のエッセンスは、先日も書かせて頂きました(→嘘をつくのは、良いこと?悪いこと?)が、次のようになります。
『 「法律」は厳格で動かすことができなかった。法を動かして人情に適合することは不可能であった。そこで・・・「事実」を動かすことを考えたのです。・・・唯一の手段は「嘘」です。あった「事実」をなかったといい、なかった「事実」をあったというよりほかに方法はないのです。』

ここで、もう一度、元号法を確認しておきますと、元号は、(A)皇位の継承があつた場合に限り (B)改める、とありますので、今回は、御譲位によって天皇の位を受け継ぐ「践祚(せんそ)」がまだ行われてはいませんでしたので、(A)の事実がない状況にありました。そこで、「内閣法制局」が用いた「嘘」が、(B)の事実はない、という主張で、(A)という大前提の条件を無視していることが理解できます。次の元号を公表しただけで、実際には変えていないから問題はない、という詭弁(きべん)です。
被保険者(保険の対象となっている人)がまだ生きているにもかかわらず、その死亡保険金を、保険金受取人が、「どうせ、いつかは死ぬんだから、いまちょうだいよ!」と生命保険会社に電話して要求することと同じ構図です。(A)死亡した場合、という大前提の条件があってこそ、(B)死亡保険金を受け取れる、わけで、(A)の事実がない状況であれば、(B)は生じない、(B)について何らかのアクションを起こす必要もないということです。
「内閣法制局」が用いた「嘘」(“解釈”)が、御理解頂けましたでしょうか?

それでは、昨日の続きとなりますが、日本政府内に存在する、私たち日本国民の敵は、「財務省」と「内閣法制局」という2つの官僚組織で、RPGのラスボスみたいなものになります。そして、このゲームの主人公こそが、私たち日本国民一人ひとりになります。そして、このゲームにおいて、そんなラスボスを倒すために必要となってくる「能力」が、「経済の論理」と「法律の論理」になります。

で、その「経済の論理」と「法律の論理」を身に付けるために、それらの基礎となっている「数学の論理」を身に付ける必要があります。
そこで、昨日の最後のところで書かせて頂きましたことを、「数学の論理」を知って頂くために確認しておきましょう。
まず、次の記事(↓)に書かれた数式の答えが何であるのかを考えてみて下さい。

☆数式に答えが2つ?
続いて、現在の算数の授業で、平然と行われている間違った教育の典型例である、次の問題(↓)について、問題そのものがどう間違っているのかを考えてみて下さい。

さきほどの記事をご覧頂くと分かるのですが、記事を書かれている方は、そもそも「数学の論理」が理解できていないのではないかと思います。「PEMDAS」のルールなどといったものも登場していますし、( )を優先するとか、前から順番に、とかといったことも書かれています。
本当に、そうなのでしょうか?
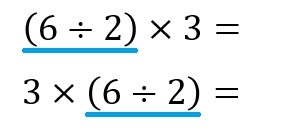
まず、上のように( )内を一つの塊(かたまり)として考えた場合(つまりは「3」になりますがw)、二つのものの「掛け算」になりますので、「掛け算には順番はありません」ので、前後を入れ替えても、その答え(=「9」)は同じになります。
それでは、( )を優先するとか、前から順番にとかといったことは正しいのでしょうか?
そこで、取り敢えず、( )を消してしまいましょう。
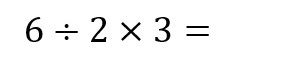
ここで、次のように順番を入れ替えた場合は、その答え(=「9」)は同じになるのですが、
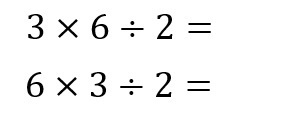
もしも、次のように順番を入れ替えた場合は、間違った答え(=「1」)になってしまいます。
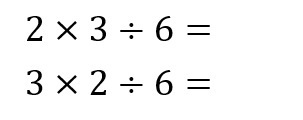
どうして、こんなことになるのかと申しますと、「÷」の意味を、世に言うところの、いわゆる“文系アタマ”では理解ができないから、ということになります(笑)
そして、そのことを糊塗(こと)し、理解(というか丸暗記w)せんがために、( )を優先するとか、前から順番にとか、とても面倒臭い方法に頼ろうとするんです。

( )があろうとなかろうと、
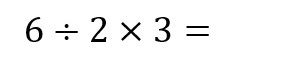
という数式の「÷2」というのを、「分数」に置き換えることで、「掛け算」だけの数式に表現し直すことができます。
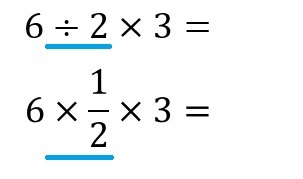
「数学」を考える際に、「四則(+、-、×、÷)」を用いるわけですが、「足し算と掛け算」だけの「二則(+、×)」の数式として捉え直すと、よりスッキリとする場合があります。
試しに、「掛け算」だけで表現された次の数式(↓)を、( )を優先するとか、前から順番に、といったことを無視して、どうぞ、お好きなように(その順番を入れ替えて)、ぜひ、計算してみて下さい。
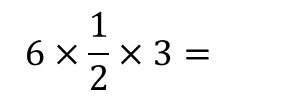
「掛け算には順番はありません」ので、すべて、その答え(=「9」)は同じになります。

で、さきほど( )を消して順番を入れ替えた場合として、その答え(=「9」)が同じになる、
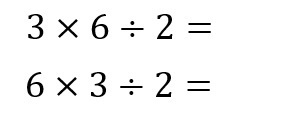
と、間違った答え(=「1」)になってしまう、
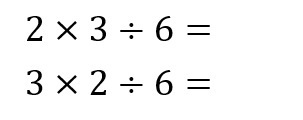
を例として挙げさせて頂きましたが、それらを「掛け算」だけの数式に表現し直しますと、
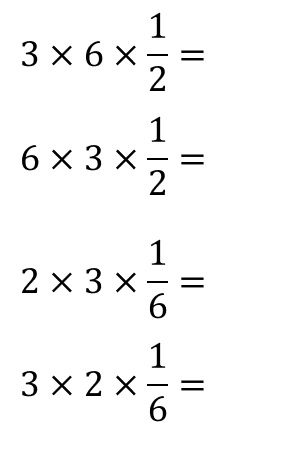
となりますが、どこが間違っていたのかが、よく理解できるのではないかと思います。
他にも、次のような、間違った答えが導かれる例も挙げておきますが、よりハッキリとその間違いに気付かれるのではないでしょうか?
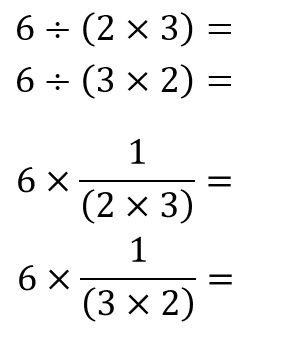
であれば、次の問題が、そもそも全くナンセンスな問題であることも、容易に理解できるのではないでしょうか? そう、「掛け算には順番はない」のですから(笑)

続きは次回に♥
ランキング参加中で~す^^ ポチっとお願いします♥
↓↓↓↓↓↓↓
にほんブログ村

人気ブログランキング


- 関連記事
-
- 憲法学通説の「戦争」 ≠ 国際法上の「戦争」 (2019/12/28)
- 「ウソ」を「本当」だと見せかける専門家 (2019/12/27)
- 国際社会や国際法を無視するのが、あの東京大学(あ)法学部なんです (2019/12/25)
- 多くの人々が勘違い&騙されるのが「通説」 ~ 「通説」と「定説」は違います (2019/12/05)
- 2019年は、「財政赤字」に対する経済学界の認識が大きく変貌する年かも! (2019/12/04)
- (問) 近代資本主義の根本は、「私的所有権」と「利子」のどちらでしょうか? ~ とあるマルキストの勘違いw (2019/12/03)
- 日本国民にはすっかり見透かされてしまっている財務省の目論見 (2019/12/02)
- ( 6 ÷ 2 ) × 3 = ? 答えはいくつでしょうか? (2019/12/01)
- ラスボスは、「財務省」と「内閣法制局」 (2019/11/30)
- お勉強を“しても”成績があがらない子供、お勉強を“しない”から成績があがらない子供、そして、“どうしようもない”子供w (2019/11/29)
- 自由民主党とは、一体何なのでしょう? ~ 自民党の国会議員が懸命にやっていることw (2019/11/28)
- マスコミの「嘘」と、“モンスターという嘘”との決定的な違い (2019/11/27)
- 嘘をつくのは、良いこと?悪いこと? (2019/11/26)
- 専制君主と立憲君主と〇〇君主 (2019/11/25)
- 皇室とコウノトリ (2019/11/24)
