2019-11-10 (Sun)

本日のキーワード : ケインズ、一般理論
『雇用・利子および貨幣の一般理論』(こよう・りしおよびかへいのいっぱんりろん、英: The General Theory of Employment, Interest and Money)は、イギリスの経済学者ジョン・メイナード・ケインズが1936年に著した経済学書。単に『一般理論』と呼ばれることもある。
当時の古典派経済学では、市場は自律的に調整されるため、最終的あるいは長期的には失業は存在しないとされていた。しかし、現実には、1929年の世界恐慌では、未曽有の大量失業が発生し、古典派経済学理論と現実との齟齬が指摘されてきた。ケインズは、本書で「需要によって生産水準が決定され、それが失業を発生させる」ことを明らかにして、経済状況を改善し、失業を解消するために、政府による財政政策及び金融政策などさまざまな面からの政策の必要性を説くだけではなく、その理論的根拠を与えた。
本日の書物 : 『数学嫌いな人のための数学 ― 数学原論』 小室 直樹 東洋経済新報社
戦後の日本人は、正しい歴史を学校で教わって来ませんでした。
そして、現代のメディアもまた、嘘の情報を流し続けています。
私たち日本人は、親日的な立場に立ち、正しく認識し直し、
客観的に情勢を判断する必要があります。
それでは、この書物を見ていきましょう!
『生徒 : 古典派が失業はないと主張する理由は何ですか。
先生 : 【セイの法則が成立するから】です。セイの法則が成立すれば、「自由市場はベスト」になりす。すなわち市場が自由であれば、すべての資源はベストに使用されることになる。労働なんていう大切な資源が使い残されることはあり得ません。完全雇用が実現されます。
生徒 : まことに論理は完全ですね。が、【その前提である「セイの法則が成立する」というところが問題】なのではありませんか。セイの法則は、必ず成立するんですか。
先生 : 【セイの法則の成立を要請(postulate)したのが古典派】です。古典派は、セイの法則を公理のように要請して、そこから多くの定理(諸法則)を導出してきました。資本主義には失業はないという命題もそれらの諸法則の一つです。

生徒 : セイの法則は成立するなんていう公理を、勝手に要請していいんですか。
先生 : どんな公理を要請しようと、理論上は、模型構築者(the model builder)の自由ですから、そこは少しもかまいません。しかし、【実証上】は、【その模型(モデル)が現実妥当性(fact fitting)を有するかどうか、模型構築者には答える責任があります】。
生徒 : そういうことですね。【大恐慌】時代には、街にも村にも、【至るところに失業者があふれかえっていた】そうですね。…失業がなくなる見込みはなかったとしたら、いくら古典派がセイの法則を振り翳(かざ)して失業なんかあり得ないと説教したところで、もう誰も聞く耳を持たなくなっていたでしょうね。
先生 : そこへ出現してきたのが【ケインズ】です。彼は、【『雇用・利子および貨幣の一般理論』】を引っ提げて登場して、【世界経済学の支配者である古典派に挑戦した】のでした。

ジョン・メイナード・ケインズ

生徒 : そして、一気に古典派を屈服させた?
先生 : そうはいきませんでした。何しろ、【ケインズの『一般理論』は難解すぎた】のでした。この本にこそ失業救済の秘策が書いてあるに違いないと人びとは飛びつきました。そして必死になって耽読(たんどく/夢中になって読む)したのでした。しかし、呆(あき)れて吃驚(びっくり)して怒り出したのでした。【あまりにも難しすぎて、ちっとも歯が立たない】。珍紛漢紛(チンプンカンプン)で何が書いてあるのやらさっぱり分からない。

【サムエルソン】は、『一般理論』の読後感を
「私は、この本を一読して少しも分からなかったことを自覚しなければ必ずや反撥(はんぱつ)していたことであったろう」
と言っているほどです。有名なストーリーです。かのサムエルソンすら分からなかった。サムエルソンの学説理解能力の高さについてはすでに神話ができているほどです。日本の高田保馬博士もケインズの『一般理論』に歯が立たなかったことについて、これまた有名な逸話があります。

ポール・アンソニー・サミュエルソン
生徒 : それほど【難解無比のケインズの『一般理論』】が、【ほんのちょっぴりの数学】で、【底の底まで分かる】んですか。
先生 : ハイ、そうです。

生徒 : ぜひ説明して下さい。
先生 : なぜ、ケインズの『一般理論』が、当時の人々には分かりにくかったのか。そこのところから始めましょう。
【それまでの経済学】は、【一つひとつの商品の需要や供給を考え】ても、【経済全体の需要や供給を考えることはありません】でした。それが【ケインズ】になって、一気に【国民全体の需要や供給から考えることにした】のでした。そこで、時代の経済学者も一般の人々も呆気(あっけ)にとられて呆然としたのでした。』

同じ式でも、全然意味が違うこともある!
いかがでしょうか?
今回ご紹介させていただく書物は、2001年に発刊されたもので、“ゆとり教育”という、後の世に大きな災いをもたらす害悪が蔓延しつつある頃に書かれた書物で、「数学」というものが如何に教育において重要であるのかが、よく理解できる良書となります。

さて、昨日の本文のところから、
〇 ケインズ理論のエッセンス = 有効需要の原理 = “方程式”
〇 古典派のエッセンス = セイの法則 = “恒等式”
というのが、「経済学の極意」であり、
〇 「特定の数値のときにだけ成立する」のが「方程式」、
〇 「どんな数値のときにも成立する」のが「恒等式」、
という風に違っているのだということが分かりました。
そこで、具体的にどのように違っているのかと申しますと、まず、本文中にも書かれていましたように、次のように「国民全体」として考えて、
国民所得(national income) : その国の国民全体の所得総額
国民生産(national product) : その国の国民全体の生産総額
国民消費(national consumption) : その国の国民全体の消費総額
国民投資(national investment) : その国の国民全体の投資総額
国民供給(national supply) : その国の国民全体の供給総額
国民需要(national demand) : その国の国民全体の需要総額
有効需要(effective demand) : 〃 (ケインズの表現)
とします。そして、
国民生産(national product) : Y [生産物(yield)の頭文字]
国民消費(national consumption) : C
国民投資(national investment) : I
とします。また、話を簡略化するために、ここでは、
国民所得(national income) = 国民生産(national product) : Y
としておきます。
古典派の考え方は、恒等式ですので、合同を表す記号の「≡」を用いて表現いたしますと、
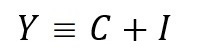
となります。他方、ケインズの考え方は、方程式ですので、
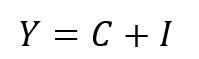
となりますが、このように、一見すると、ほとんど違いがないように感じられるのですが、実は、まったく“正反対”の考え方になっているんです。
古典派の「資本主義には失業はないという命題」に対して、マルクスは「資本主義であれば失業が生じる」という反証を、自ら証明してみせて、見事に論破していました。ただし、マルクスの理論の循環論的な欠陥を指摘されたことによって非難され、異端扱いされることになります。そして、そのマルクスの理論を不正確に勝手な解釈をしたマルキストらが、世界中で「強盗」「レイプ」「放火」「殺人」・・・等々、ありとあらゆる犯罪を犯しながら、「資本主義を無くしさえすれば、失業者はなくなる!」といった勘違いも甚だしい屁理屈を根拠に、“暴力を正当化”したわけです。
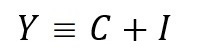
古典派の考え方、つまり、「セイの法則」では、供給すれば売れる(Demand on supply.)、供給はそれ自身の需要を作る(Supply creates its own demand.)としているわけですから、左辺の供給によって右辺の需要が恒(つね)に等しくなる、ということになります。

国民生産が500兆円あれば、国民需要も500兆ある、という風に解釈されるわけです。

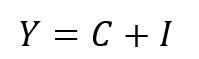
他方、ケインズの考え方は、つまり、「有効需要(effective demand)」では、
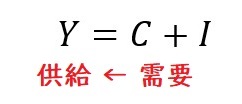
有効需要が500兆円あれば、国民経済は、需要に見合う分の供給をするので、国民供給が500兆円になると、需要と供給のバランス(均衡)がとれてイコールになる、という風に解釈されます。
そして、重要なのが、この方程式は、「均衡のときに限って成り立つ」という点であり、均衡が必ず存在するとは限りませんし、また解が存在するとも限りませんし、さらに、成立するとも限らない、ということになります。だからこそ、方程式であるわけです。

ちなみに、マルクス経済学で言うところの「再生産」という概念がありますが、マルクスは、その再生産図式において、「セイの法則」を前提として理論を進めていますので、所詮、マルクスも恒等式で考えていたということになります。しかし、何故か、そんなことも知らずに、「マルクスすげぇ!」って妄信する人(世界的にもバカにされるのですがw)が、困ったことに、ほんの僅か存在しています。

ハッキリと申し上げますと、マルクスの理論を勝手な解釈で理解したつもりでいるヒト(例:ewkefcとか)がいるのですが、恐らくマルクスの本を読んだこともなく、仮に読んでいたとしても理解さえできないので、ケインズの『一般理論』となると尚更、理解できるはずもないことになります。ということは、ケインズ理論を再解釈した、現代経済学におけるポール・クルーグマンの理論なんて、恐らく知らないのだと思います。だって、100年以上前のマルクスの理論でさえ、理解できていないわけですから、小学校低学年の算数が理解出来ないので、大学・大学院の数学科の授業が分かりません、と至極当然のことを“恒等式”のように表現することができるわけです。

それでは、ここからは、昨日の続きに入らせて頂きます。
昨日のところで、特別な数であるネイピア数「e」を底とする対数、
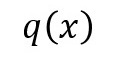
※教科書などでは、次のような記号で表現されている「自然対数」と呼ばれるもの
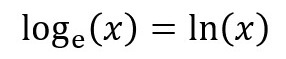
をn回微分したときの導関数が、
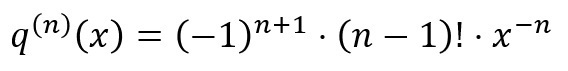
となることが分かりました。ところが、いま、「q(x)」の「x=1」における微分係数(=導関数)である、
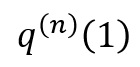
を求める必要があるんです。そこで、
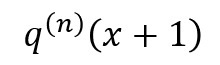
だとどうなるのかを考えます。まず、
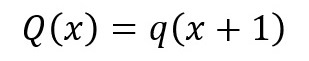
と置きます。すると、その導関数は、「q(x)」の導関数(=微分係数)に「x+1」を入れただけのものとなるはずです。
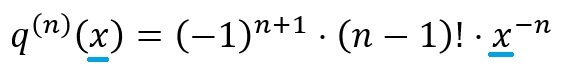
ということは、n≧1のときには、
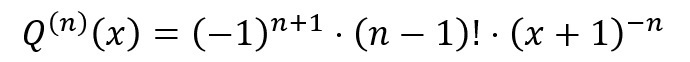
と表すことができることになります。で、いま知りたいのが、
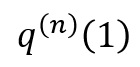
なのですが、これは、
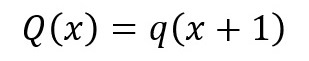
の「xをゼロ」としたものと同じになりますので、
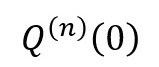
を
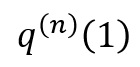
と言い換えているだけのことになります。ですので、さきほどの数式の「xをゼロ」とすると、n≧1のときには、
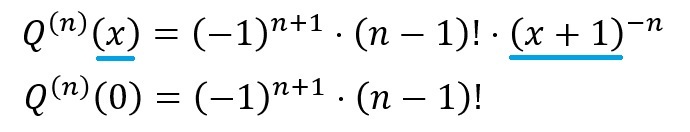
となるということが分かりました。また、n=0のときには、
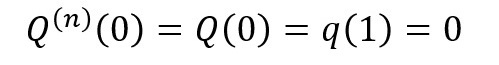
となります。で、ここまでに判明したことを、いつもの“あの函数(関数)”に用いてみようと思います。
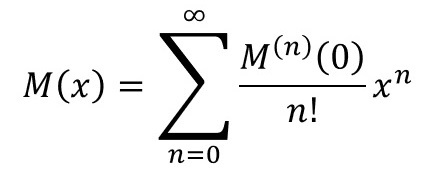

続きは次回に♥
ランキング参加中で~す^^ ポチっとお願いします♥
↓↓↓↓↓↓↓
にほんブログ村

人気ブログランキング


- 関連記事
-
- 「悪夢の民主党政権」の生みの親は、財務省の部下・麻生太郎です(笑) (2019/12/16)
- ミルトン・フリードマンを“シカト”する日本の「御用経済学者」・「ガラパゴス経済学者」たち (2019/12/14)
- 資本主義に代わるものなんてない!! タイラー・コーエンも批判する、お馬鹿なマルキストの単純志向 (2019/11/18)
- 国会議員の皆さんへ ~ 「日本国憲法」の第43条って、どんなことが書かれているのかご存知ですか? (2019/11/17)
- アクセルとブレーキを踏み間違えてはダメ!!! (2019/11/16)
- 資本主義に代わるシステムはありません!! ~ マルキストがなぜ馬鹿にされるのか、その分かりやすい理由とは? (2019/11/13)
- “マルキストの阿呆(あほう)”には到底理解ができない、ケインズ派と古典派の分かれ道 (2019/11/11)
- マルクスの理論すら理解できないなら、ケインズの理論は到底理解はできません (2019/11/10)
- 「市場に出した品物はみんな売れる」という法則 (2019/11/09)
- 学校教師が理解していない、「方程式の解」と「恒等式の証明」 (2019/11/08)
- 方程式と恒等式のちがいってナニ??? (2019/11/07)
- 桶屋が儲からないようにするために ~ マルクスの主張とは異なる、マルキストの勝手な思い込み (2019/11/06)
- マルキストは、マルクスの学説を理解していなかったんです ~ マルクスの言っていることは何? (2019/11/05)
- カール・マルクスが研究していたのは、「社会主義経済の研究」ではありませんwww (2019/11/04)
- “左翼”止めますか?それとも、人間やめますか? (2019/11/03)
