「武漢肺炎（COVIT-19）」の“ウイルス”って、無限に増殖することは可能なの？

2020-03-24 (Tue)

本日のキーワード　：　コックス報告書

一般にクリス・コックス下院議員に因んでコックス報告書として知られる合衆国安全保障並びに中華人民共和国との軍事・経済問題に関する特別委員会報告書は中華人民共和国による1980年代から1990年代にわたった合衆国内における秘密活動に関しての報告書であり、機密扱いの合衆国政府文書である。

本日の書物　：　『中国の情報機関 ―― 世界を席巻する特務工作』　柏原竜一　祥伝社

戦後の日本人は、正しい歴史を学校で教わって来ませんでした。

そして、現代のメディアもまた、嘘の情報を流し続けています。

私たち日本人は、親日的な立場に立ち、正しく認識し直し、

客観的に情勢を判断する必要があります。

それでは、この書物を見ていきましょう！

『　【中国人民解放軍情報部】が【最も激しい攻撃を仕掛けている】のは、やはりなんといっても【アメリカ】であろう。

☆米2議員、ツイッター社に共産党幹部の参加禁止求める　偽情報拡散を問題視

　【アメリカにおける中国の情報活動】を語る上で、忘れることができないのが【『コックス報告書』】である。これは、１９８０年代から１９９０年代にかけて、中国がアメリカ国内で行った秘密活動に関する報告書で、米下院に提出された。１９９９年５月２５日に発表されたこの文書は、【中国による技術剽窃（ひょうせつ）】がどれほど大規模なものであるかを明らかにしたのだった。

☆House Report 105-851 - U.S. National Security and Military/Commercial Concerns with the People's Republic of China

　【コックス報告書の結論】は、驚くべきものであった。【１９７０年代以来、中国は、ミサイル誘導コンピューター、中性子爆弾、多弾頭式核弾頭、レーザー研究などといったアメリカの国防機密を盗んできた】、というのである。しかも、これらの技術の剽窃（ひょうせつ）は、中国が独力で成し遂げたものではなかった。報告書によれば、【アメリカの企業が、自らがパートナーとなる合弁会社を設立することによって、重要な技術を中国に提供していた】のである。それ以外にも、【特許や技術上の計画などが、無防備ゆえに、中国側に流れている】というのだ。…

☆House Report 105-851 - U.S. National Security and Military/Commercial Concerns with the People's Republic of China

　コックス報告書は、【なぜ中国がこれらの情報を収集するのか】、その目的も分析している。【その目的】とは、【人民解放軍の近代化】であり、近代化の対象は、戦場での通信装備、（航空機もしくは他の手段による）偵察、宇宙兵器、可動式核兵器、攻撃用潜水艦、戦闘機、誘導兵器、急速展開地上部隊の訓練といったものであった。

クリストファー・コックス（Christopher Cox）

　このように目標を評価した後に、クリストファー・コックスと彼の同僚のレポート作成者は、アメリカ国内の専門家やアメリカに亡命した中国人の証言を基に、【秘密エージェントの特殊な役割】を明らかにした。

　主に技術の取得を担当している【中国のプロの情報機関】は、【国家安全部】と【総参謀第二部】である。

　さらに、これらの情報機関とは別に、【中国】は、【民間や軍の研究所、それに企業といった別の国家機構を利用した素人（しろうと）による技術収集に精力を傾けるようになっている】。非常に多くの【米国技術の流出】は、国家安全部や人民解放軍総参謀第二部の下での作戦によるものではなく、【アメリカと中国の間の大学や学術、それに商業上のやりとりを通じて生じている】のである。

　国家安全部もしくは総参謀第二部のプロのエージェントは、海外における科学技術収集に関しては何の障害も感じていない。大部分の情報は、情報収集計画の点では、【学生や科学者、研究者、それに西側への旅行者といった素人のエージェントを通じて収集】される。表向きは、彼らは研究機関や科学機関、委員会、それに企業を代表しているが、【これらの個人は、しばしば、当局の指示に従って活動する】。

彼らは、ある分野で情報収集を行うと、民生部門もしくは軍事部門での別の情報に出会う。こうして【芋づる式に情報が収集される】のだ。

　中国の情報活動の行動様式に精通していない情報機関の関係者は、中国もまた他の国と同様に情報機関が秘密作戦を指揮しており、すべての秘密工作は、必然的に、情報機関によって指揮されているという結論を下すことが多い。中国の場合には、必ずしもその規則にはよらないのである。

　このように【アメリカにおいては、総参謀第二部は国家安全部と協力し、膨大な軍事科学技術情報を盗み出している】。では【日本の場合はどうなの】だろうか。』

「泥棒」が先？　それとも「嘘つき」が先？

いかがでしょうか？

今回ご紹介させていただく書物は、「武漢肺炎（COVIT-19）」を世界中に拡散させた、無能な指導者が率いる“中国共産党”とその支配下にある“人民解放軍”並びに“中華人民共和国”の「情報機関」（諜報機関・スパイ）の実態が理解できる書物で、現在、我が国で見られるような「“親中国共産党”のジャーナリストや学者」が何故存在しているのかが分かる良書となります。

さて、本文をご覧頂いて、中華人民共和国というものの本性が、非常に良く御理解頂けたのではないかと思いますが、その中華人民共和国の上に立ち支配（＝指示命令）している中国共産党という組織は、先端技術の「剽窃（ひょうせつ）」を平気で行う組織、つまり「盗人集団」であり、また、平気で「嘘をつく」能力に秀でた組織になります。

石平の自慢話
３月１９日　ニューズウィーク日本語版サイトが石平論考「中国新規感染者数ゼロの怪」を掲載。
３月２０日　共同通信、「武漢の改善、欺瞞と医師が告発」
３月２１日　毎日新聞、「新規国内感染を”ゼロ”にし続ける中国政府発表のからくり」
３月２２日　テレ朝「当局発表”ゼロ”に疑問」
— 石平太郎 (@liyonyon) March 22, 2020

☆新型コロナ：中国「新規感染者数ゼロ」の怪

☆＜独自＞中共肺炎、武漢市の3月14日の新規感染者は公表の約22倍

そんな中国共産党の実態を見ていますと、「泥棒」が先なのか「嘘つき」が先なのか、混乱してしまうのですが、やっぱり「嘘つき」の方が先なんでしょうね💗

We must not allow disinformation to undermine our efforts to fight #coronavirus. We're delivering good outcomes for the American people and will continue to do so. I encourage all Americans to go only to trusted sources such as @CDCgov and @TravelGov for reliable information. pic.twitter.com/lV0e55ZzPI
— Secretary Pompeo (@SecPompeo) March 20, 2020

Disinformation is not only coming from random actors around the world - but also from the Chinese Communist Party, Russia, and the Iranian regime. We must not permit these efforts to undermine our democracy, our freedom, and how we're responding to the Wuhan Virus. pic.twitter.com/WtB2Isrkkf
— Secretary Pompeo (@SecPompeo) March 20, 2020

☆【米国：警告】ポンペオ：COVID-19についての偽情報は、中共・露・イランからも発信！

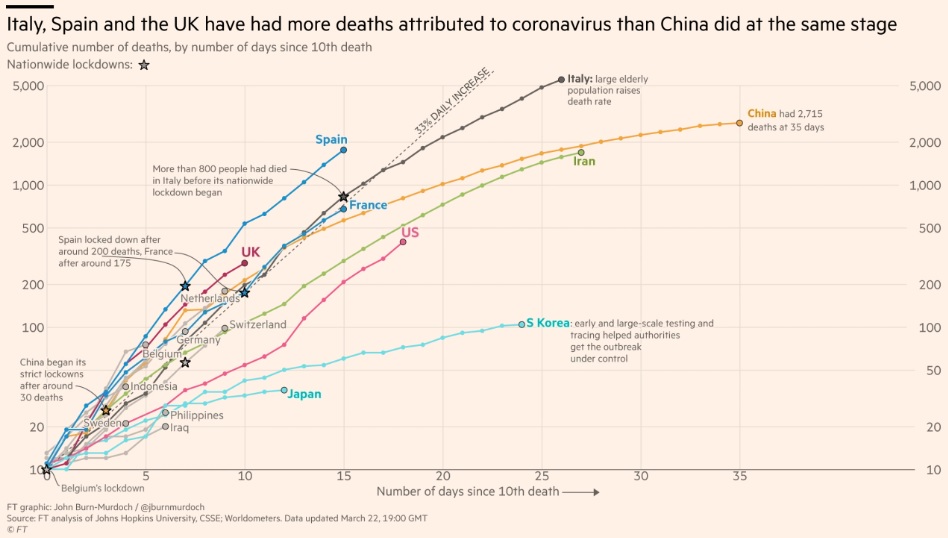
☆Coronavirus tracked: the latest figures as the pandemic spreads

それでは、ここからは昨日の続きに入らせて頂きたいと思いますが、世界中で大騒ぎになっている「中国ウイルス」による「武漢肺炎（COVID-19）禍」ですが、ただ単に騒いでいても、何ら発展性がありませんので、中国共産党によって撒き散らされたウイルスの犠牲者に報いるためにも、私たち日本国民はこの経験から何かしらを「学ぶ」ことが必要だと思っています。

そこで、この機会に少し、「数学」的に考えることを試みようと、先日から書かせて頂いているところになります。

詳しくは、昨日までに書かせて頂いたものを遡（さかのぼ）ってご確認頂きたいのですが、今回の「中国ウイルス」による「武漢肺炎（COVID-19）禍」には「指数関数」は使えない、にもかかわらず「指数関数的に」みたいな表現が散見されます。

繰り返しになりますが、いま仮に、ある細菌がその時々の量に比例して増殖するものとします。

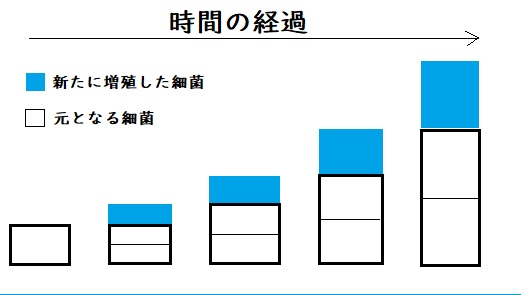
その増殖する細菌の時刻「ｔ」における量を「ｙ」とし、この細菌の時刻「 0 」における量を「 1ｇ」、また、その時点（→時刻「 0 」の時点）での細菌の増加率が「 0.5 」であったと仮定します（→つまり、その時点での細菌の量の50％が増加する）と、次の微分の法則が成り立ちます。

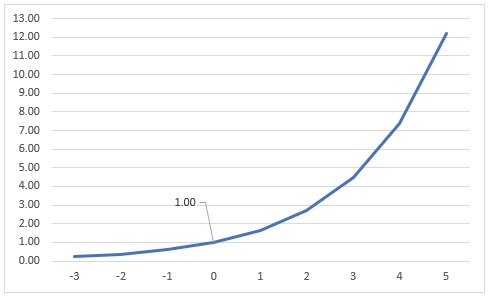
ｙ´＝0.5ｙ　、　ｔ＝0 のとき y=1　　・・・・・①　

その函数（関数）をグラフで表しますと、次のようになり（→横軸が「 t 」、縦軸が「ｙ」で、ｔ＝0 のとき y=1 になります）、

数式で表しますと、次のような「指数関数」になります。

ある量が増大する速さが増大する量に比例する現象のことを、「指数関数的成長（exponential growth）」と呼ぶのですが、それを数式で表現致しますと、次のような「微分方程式」になり、

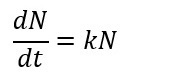
この「微分方程式」を解くと、

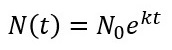
となります（Ｎ0＝Ｎ（0）は初期値を意味）。

実は、昨日書かせて頂いた、１８世紀末から１９世紀初における、イギリスの古典派経済学を代表するする経済学者であるトマス・ロバート・マルサスが、その著書『人口論』で、人口は原理的に“指数関数的”に増加することを指摘していたのですが、その論理の根拠となる前提を突き崩されることになります。

それは、非常に素朴な疑問から来るものだったのですが。。。

トマス・ロバート・マルサス

それを実感して頂くためにもお考え頂きたいのですが、ここで、もう一度、細菌の増殖のお話に戻らせて頂き、その細菌の増殖が、

と表されるものとして、「ｔ」を、いま仮に「２４時間（１日）」であったとすると、答えはいくらになるでしょうか？

また、「ｔ」を、いま仮に「１６８時間（１週間）」であったとすると、答えはいくらになるでしょうか？

その「解」を求めるためには、何かが必要となってくるのですが。。。

もう、お気付きですね💗

息子の質問
「100分の1で当たりが出るくじを100回やったら、1回は当たる確率ってどれくらい？」
「そうだなぁ。1-(99/100)^100だから、だいたい1-1/eなので、2/3くらいだな」
「やっぱり。もっと1に近いと思ってたんだけど、なりそうになくて、不思議だったんだけど、ちょっとまって、そのeって何？」
— 濱中裕明 (@Ototo_) March 22, 2020