2019-04-09 (Tue)

本日のキーワード : 迷信
迷信(めいしん、英: superstition)とは、人々に信じられていることのうちで、合理的な根拠を欠いているもの。一般的には社会生活をいとなむのに実害があり、道徳に反するような知識や俗信などをこう呼ぶ。様々な俗信のうち、社会生活に実害を及ぼすものである。
本日の書物 : 『日本の国という水槽の水の入れ替え方―憂国の随想集』 岡潔 成甲書房
戦後の日本人は、正しい歴史を学校で教わって来ませんでした。
そして、現代のメディアもまた、嘘の情報を流し続けています。
私たち日本人は、親日的な立場に立ち、正しく認識し直し、
客観的に情勢を判断する必要があります。
それでは、この書物を見ていきましょう!
『 光が戦備を整えようとすると、【一番問題になる】のは【日本の教育】である。学校、社会、家庭がみな問題になる。この教育体系では、【学校だけでは教育できない】。

これ(学校教育)を急速に変えようにも何よりも、先生の数が恐ろしく足りない。

私は学校教育について、【文部省】も、たとえば【日教組】も、なぜこんな無茶ばかりするのかわからなかった。それについていろいろ注意しても、どうしても【わかってもらえない】らしい。

☆東京新聞「繰り返し風俗店に通ったりする行動は依存症で病気 今すぐ治療を」~ネットの反応「お前らが聖人扱いしてたビーチ前川はどうなんだよ?」「官房長官依存症がお前のところに居るだろw」
なぜこういうことになるのか、それを的確に知らなければ手のつけようがない。ながい間それを捜し求めた。そして最近になってやっとわかった。
日本人は【学校教育】とは【学問を教えることだと信じて疑わない】のである。どうも【明治の初めからそう】なのである。…

私がついに探り当てるのに成功したときの、私のやり方をお話ししよう。
日本民族は非常にすぐれた民族であるのに、【物質文明(広義)】に接すると、いつも【インフェリオリティ・コンプレックス(Inferiority complex/劣等感)】にとりつかれてしまう。前に支那文明に対しそうであった。その結果、大弊害をこうむる。

大多数が、インフェリオリティ・コンプレックスになぜとりつかれるのだろうというのも、興味のある問題には違いないのだが、当分いりそうにも思えない。急を要するのは、【そのよろめきの結果】が、【どんな形でいま国中に残っているか】、ということを調べることである、
日本は明治の初め、必要から大急ぎで【西洋文明】を取り入れて、【それによろめいた】。衆目の見るところである。【その後遺症】の残っていないはずはない。そうすると第一に目についたのが、【「学問恐怖症」】。

ほかにもいろいろあるだろうが、そう一時にいっても役に立たない。一つずつ片づけていこう。
【学問恐怖症】からくる【一番大きな害】とは何だろう。【「学校教育とは学問を教えることだと思ってしまうこと」】――こうしてやっと探り当てたのである。

これでみなわかる。念のため数人の人に聞いてみたが、果たして【みなそう思い込んでしまっている】のである。

そうすると、【日本の今の学校教育】は、実に驚き入った【迷信】だということになる。
そこから説明しよう。』

「教育」の「育」の意味
いかがでしょうか?
今回ご紹介させていただく書物は、日本を代表する天才数学者である著者による書物で、これまでにも何冊がご紹介をさせて頂いておりますが、明治時代の途中から様相の変化が現れ、大東亜戦争の敗戦、さらには屈辱的な占領期を経て、いわゆる戦後から現代に至る私たち日本の問題点を正しく指摘されている良書であり、その一方で、それら諸問題について一向に改善されていないという現実を知ることや、これからの私たち日本人が何をしなければならないのかを学ぶことが、本書を通じて可能となります。

さて、著者は、現代の私たち日本の教育体系では、「学校だけでは教育できない」と断言されているわけですが、当ブログの考えでは、「もはや(既存の)学校では教育できない」というところまで到達しているのですが、果たして、皆さまはどのようにお考えでございますでしょうか?
本文中に書かれていましたが、「何よりも、先生の数が恐ろしく足りない」という部分を、単に「頭数を増やせば良い」と考えて、自分たちの保身や利益追求に一生懸命なのが三流官庁と呼ばれる文部科学省で、あの前川喜平なる歴史上にその汚名を残し続けるであろう「変態(ヘンタイ)」を産み出した官僚組織が、日本の教育制度を国家統制している時点で、すでに期待はできないということが明らかだと思います。



また、「学校教育」を「学問を教えることだと信じて疑わない」、つまり勘違いしてそう思い込んでいるバカが居る、と著者は批判されている(もちろん、文部科学省や日教組のことですがw)のですが、まさしくその通りだと思います。

「教育」という言葉は、「教」と「育」という記号に過ぎない漢字の組み合わせになりますが、もし、「学問を教えること」を主として考えるのであれば、「教学」という表現で十分です。

という記号に過ぎない漢字は、旧字で、

と書くのですが、そこに見られる「×」みたいなものは、神社で見られる「千木(ちぎ)」を表したもので、


という記号に過ぎない漢字も、旧字で、

と書き、そこに見られる「×」みたいなものも同じです。
詳しくはこちらをご参照💗
↓
☆『漢字の語源「教・育」』

で、「教育」という記号の中にある「育」という記号を、私たち日本人の和語(やまとことば)で申しますと、「はぐくむ」になります。
「はぐくむ」は、「は(羽)」と動詞の「くくむ(含む)」から成る言葉で、親鳥がひなを羽で包み込んでかばい育てるという意味になります。

であれば、「教育」の意味するところは、「はぐくむ」こと・そのやり方を子どもたちに「教える」のでしょうか?

ここで、アタマの悪いおバカなパヨクは、こう考えてしまいます。
教育 = 教える×学問 + 育てる
子どもたちに「教える」。
何を? 学問を。
子どもたちを「育てる」。
何処で、誰が? 学校、社会、家庭すべてで。
こんな感じです。少し分かり難いでしょうか?
当ブログの考えでは、
教育 = (子どもたちから)教えてもらう + はぐくむ(育む)
となるはずですし、それが当然なのですが。

本日の課題 : 計算ではなく図を見て考えよ!
それでは、ここからは昨日の続きである「微分積分学」を自ら発明する、という無謀なチャレンジの続きに入りたいと思います。
「微分積分学」のエッセンスは、何度も繰り返しますが、
『「曲がった」ものも、どんどん拡大すると、「まっすぐ」に見えてくる』
ということになります。

さて、昨日までのところで、円周(「r」は半径)が、
であることを応用して、「水平方向(h)」と「垂直方向(v)」を決め、長さ「ℓ」の線分が、正の水平軸から「反時計回り」に「角度(α)」を成しているとし、
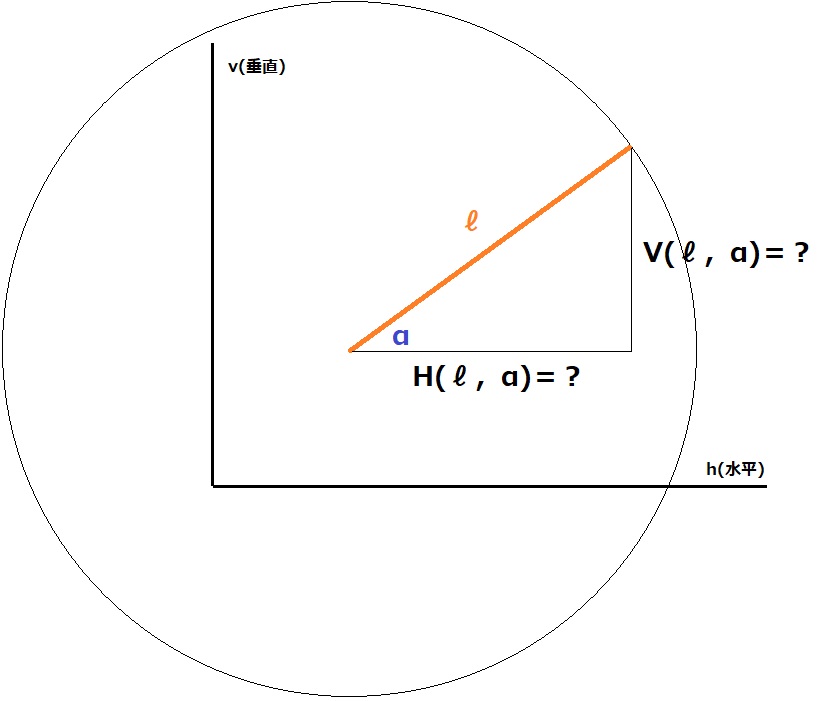
どれくらい水平方向で、また、どれくらい垂直方向であるのかを、アレコレと考えた結果、それぞれ次のような略号で表現することにしました(勝手に決めました!)。
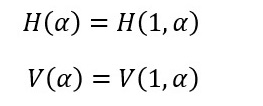
そして、その「角度(α)」を次々と変化させていくと、円ができることになります。
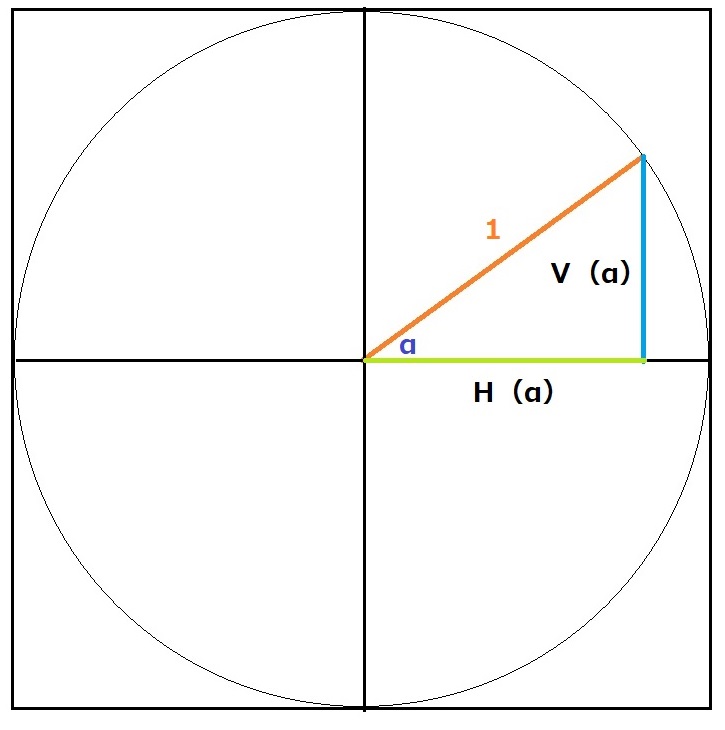
そして、ここからは計算の必要もなく、ただ図を眺めるだけでご理解頂けるのですが、「角度(α)」がゼロであれば、
どれくらい水平方向で、また、どれくらい垂直方向であるのかは、次のように表現することができます。
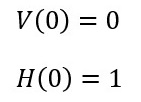
また、「角度(α)」が4分の1回転した「2分のπ」であれば、
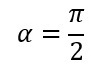
どれくらい水平方向で、また、どれくらい垂直方向であるのかは、次のように表現することができます。
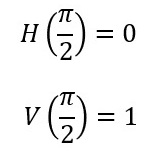
さらに、また、「角度(α)」に「2π」を加えると、1回転することになりますので、
次のように表現することができます。
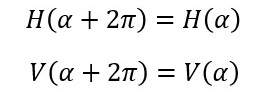
さて、ここまで整理できたところで、相変わらず、角度(α)に対するH(α)やV(α)の計算方法はサッパリ分からないままなのですが、
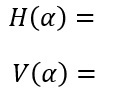
それらを「微分する(導関数を求める)」ことは可能なのでしょうか?

どうすれば良いのか、ぜひ皆さまも考えてみて下さい。
続きは次回に♥
ランキング参加中で~す^^ ポチっとお願いします♥
↓↓↓↓↓↓↓
にほんブログ村

人気ブログランキング


- 関連記事
-
- 「文系の経済学」と「理系の経済学」 マルクス経済学はどっち? (2019/06/30)
- 何が正しい経済理論なのか“サッパリ”分からない日本人 ~ 例 : 実物的景気循環論(RBC) (2019/06/29)
- マルクスよりも愛された社会主義者らのアイドル ~ 「国家社会主義者」のラッサール (2019/06/18)
- この5年間で、何ら「学習」出来なかった日本政府 ~ お子さまでもわかる「消費税率引き上げ」が絶対にダメな理由 (2019/06/17)
- 「サタニズム(悪魔崇拝)」の「マルクス教(=共産主義)」の布教活動 ~ 使徒・片山潜 (2019/06/14)
- 西洋的自然科学にみられる決定的矛盾 (2019/04/11)
- 教育とは、決して、「学問を教えること」ではありません (2019/04/10)
- 日本の今の学校教育は、単なる「迷信」です ~ 学問恐怖症の弊害 (2019/04/09)
- 日本民族と「平等性智」 (2019/04/08)
- 莵道稚郎子命(うじのわきいらつこのみこと)と毛沢東との決定的な違い (2019/04/07)
- 「平成時代の幕開け」と「朝日新聞」と「ソ連崩壊」 (2019/03/25)
- 偽物の経済学であるマルクスの理論を破壊した、経済学の本物の革命 (2019/03/22)
- 日本共産党とソ連のスパイ (2019/03/21)
- 「大化の改新」は、何のために必要だったのでしょうか? なぜならば、・・・ (2019/03/20)
- アメリカに一方的に命令される「中国」と「北朝鮮」 (2019/03/19)
