日本のお札の材料となっている「フィリピンの名産品」って何でしょう？

2019-01-09 (Wed)

本日のキーワード　：　ダバオ麻

マニラアサ（マニラ麻、学名：Musa textilis）はバショウ科バショウ属の植物。丈夫な繊維が取れるため、繊維作物として経済的に重要である。

名称の「マニラ」は原産地であるフィリピンの首都・マニラに由来する。分類上はアサの仲間ではないが、繊維が取れることから最も一般的な繊維作物である「アサ」の名がついている。他にアバカ、セブ麻、ダバオ麻とも呼ばれる。

マニラアサの繊維は植物繊維としては最も強靭なものの1つである。またマニラアサは水に浮き、太陽光や風雨などに対しても、非常に高い耐久性を示す。船舶係留用などのロープを始め、高級な紙（紙幣や封筒）、織物などに用いられている。日本銀行券の紙幣もこれにあたる。

第二次世界大戦前の日本人も、フィリピンのミンダナオ島ダバオ市に渡り、麻栽培従事者が2万人に及んだ。その後設立された日本人墓地があった慰霊碑の前で、2013年にロドリゴ・ドゥテルテ大統領が、地域経済の発展に寄与したと評価する挨拶をしている。

日本銀行券の原材料には、和紙と同じく三椏（ミツマタ）と、耐久性向上のためマニラ麻が使用されている。これは、繊維が頑丈で独特の手触りがあるために、偽造の防止にも効果があるためである。

本日の書物　：　『アメリカの「反中」は本気だ！』　宮崎正弘　ビジネス社

戦後の日本人は、正しい歴史を学校で教わって来ませんでした。

そして、現代のメディアもまた、嘘の情報を流し続けています。

私たち日本人は、親日的な立場に立ち、正しく認識し直し、

客観的に情勢を判断する必要があります。

それでは、この書物を見ていきましょう！

『　２０１８年２月に、筆者は【ミンダナオ】に行った。【ミンダナオ諸島はイスラムが強い】うえにルソン島の主流言語である【タガログ語が通じない】。

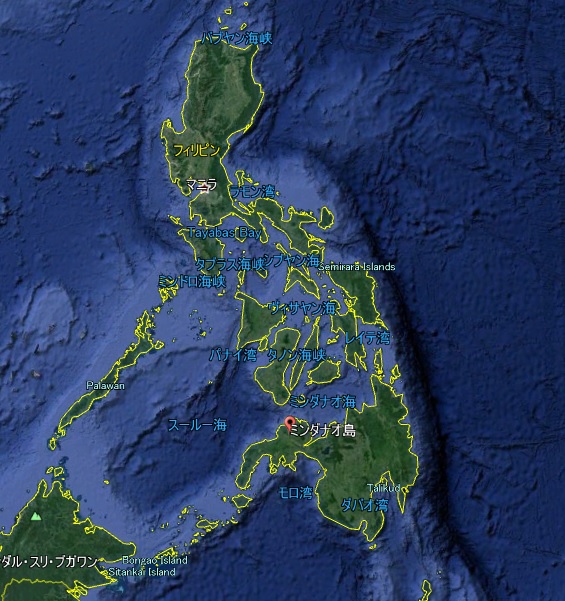
　第２の都市、【ダバオ】は周辺を含め【５００万都市】に変貌している。【ここで通じるのは現地の言葉】である。あちこちで新築ビル、マンション建設の槌音（つちおと）高く、年金生活をダバオに求めてやってきた日本人老夫妻にも何組か出会った。しかし【イスラム教のモスクはほとんど見かけない】。

　ミンダナオの都市部では英語が通じると旅行ガイドブックに書かれているのだが、それも観光ガイドとかホテル、高級レストランの話である。ローカルな市場へ行けば、タガログ語さえ通じない。

　セブン・イレブンが方々にあり、コンビニ文化が同時に浸透しつつあることは意外だった。行き当たりばったりにタクシーを拾った。ちゃんとメーターで走るタクシーはトヨタが多く、運転手は片言の英語を理解する。だからたいがいの用は足せる。

　それより驚いたのは【ダバオ】は【日本の影響がえらく強い】ことだった。

　街角に建つ【外国語学校】。【盛況は英語、日本語】で、中国語、韓国語の選択は少ない。スペイン語は語学研修施設から消えている。

　【ダバオの町】には【マニラ同様に十数もの日本料亭がある】が、「吉兆」とか「日本か」とかの命名ではなく、【「隊長」とか「将軍」とか、軍隊用語を店名にしている】。これは【ダバオ独特】である。

　【理由】はすぐにわかった。

　【ダバオの郊外】、とくに【カリナン】あたりに【「日本人村」が存在していたから】だ。

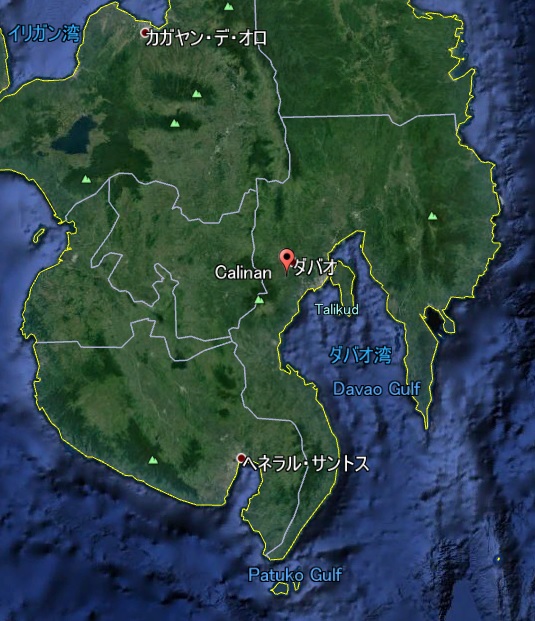
ダバオの日本人街（1930年代）

ダバオの日本人学校（1939年）

☆（特活）日本フィリピンボランティア協会（Japan Philippines Volunteer Association - JPVA）facebook

☆ダバオ案内所

　マニラの日本人街は秀吉のキリシタンバテレン追放によって漂流的な亡命をした高山右近の時代に存在した。堺商人らが貿易で見てマニラに出入りしたし、当時の遣欧使節はかならずマニラに寄港した。

　いまマニラの下町＝パコ駅周辺にその残骸も面影もなく駅前の小さな公園に立つ高山右近像は道路工事のため緑色の網がかけられていた。しかも付近の人は誰もタカヤマウコンと言ってもわからなかった。

Plaza Dilao

　ところが【ダバオ】には戦争中の兵站（へいたん）基地だった【「日本トンネル」】（防空壕も兼ねた地下要塞跡）が残り、戦争中は全長８キロもあった。そのうち２００メートルが公開され、兵舎、塹壕（ざんごう）、坑道が見学できる。ガイド付き入場料は５０ペソ。しかもこの施設内にはビジネスホテルが建っている。

　【大東亜戦争】でフィリピンが舞台となった【激戦地】はコレヒドール、レイテだが、【ミンダナオ】も激戦地だった。２０１７年に【安倍首相が訪問】したとき、【ドゥテルテ大統領のダバオの自宅で晩餐会】が行われたが、翌日、【昭恵夫人】が【これら激戦区跡、日本人墓地を慰霊に訪れている】。…

　【ダバオ】は【ドゥテルテ大統領の地盤】であり、【その人気は圧倒的】である。ドゥテルテ大統領は【麻薬撲滅】を掲げて【密売人をばんばん銃殺】し、恐れをなしたマフィア構成員の多くが自首した。このため刑務所が満杯となった。』

フィリピン　ダバオの最近のニュース

いかがでしょうか？

今回ご紹介させていただく書物は、当ブログでも度々ご紹介させて頂いております、当代随一のチャイナ・ウォッチャーである著者による、優れた「良質なる情報」が詰まった良書となります。ぶっちゃけ、朝日新聞などのサラリーマン記者は、自分の足で「情報」を得るなどといった面倒なことをやらないので、「コピペ」をするか「捏造」するかという二者択一で、やっつけ仕事の記事を日々描き続けるという、とんでもなく愚かで退屈なルーティン・ワークを、何ら疑問視することなくやり遂げることができるそうなのですが（ひょっとしたら、それがご自慢なのかもｗ）、そんな愚者とは違って、お金を出して買う意味がある著者の書物は、幅広く私たち日本人が共有すべきものではないかと考えており、お薦めの書物となります。

さて、昨年末のミンダナオ島は地震やら爆破騒ぎなど、なにかと話題になっていました。

☆フィリピン南部でM6.9の地震、最大30センチの津波の可能性

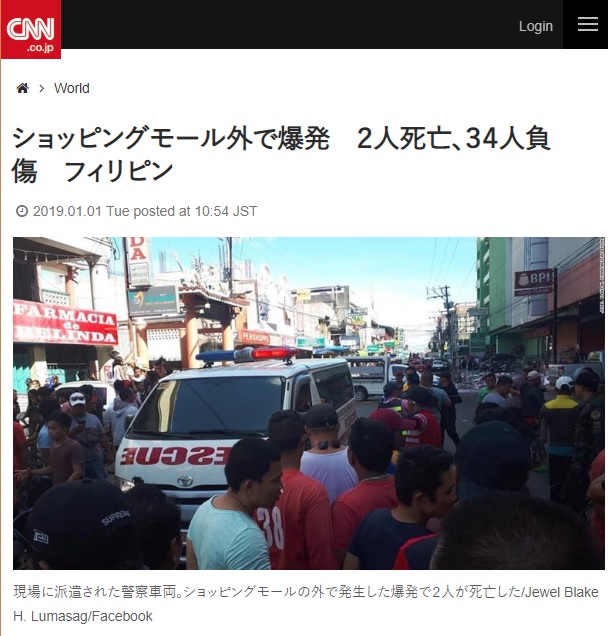
☆ショッピングモール外で爆発　２人死亡、３４人負傷　フィリピン

それは兎も角、安倍総理を熱狂的に迎えてくださったダバオには、まだ行ったことがありませんので、一度行ってみたいなと思います。子どもたちの受験の関係で、当面は行けそうにはないのですが。。。

本日の課題　：　（問）　三角数の中に平方数になるものは無数に存在するか？

それでは、本日は早速、昨日の続きに入りたいと思います。子どもたちだけに、お勉強を頑張らせるわけにはいきませんので、大人である私たちも、本当のお勉強をみせてあげるつもりで、「数学」や「歴史」を考えていきましょう。

昨年の暮れから、次の問題について考えているところになります。

（問）　三角数の中に平方数になるものは無数に存在するか？

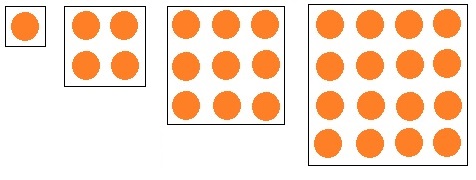
平方数の例

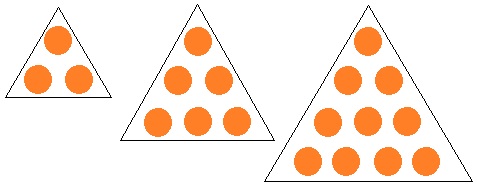
三角数の例

つまり、「平方三角数」が無限に存在するのかどうか、ということを考えているところです。

そして、平方数の式を「ｎ」を使って、三角数の式を「m」を使って、次の式を得ました。

①　2×(2n)² = (2m + 1)² -1

ここで、「平方三角数」となる数を求めるために、

②　y = 2n、x = 2m + 1

と置き換えました。

①に②を代入して得られた式が、次のものになります。

③　x² - 2ｙ² = 1

さらに、そこから得られた式が、次のものになります。

④　(x + ｙ√2)(x - ｙ√2) = 1

③と④の式から、次のように表すことができます。

⑤　x² - 2ｙ² = (x + ｙ√2)(x - ｙ√2)

実際に Excel を使って調べてみたところ、３つの平方三角数、「１」と「３６」と「１２２５」を発見することができたのですが、

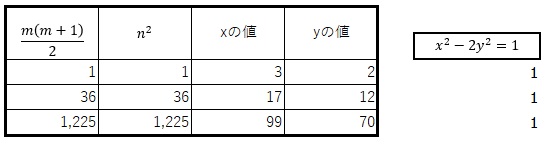
「平方三角数」に対応する「xの値」、「yの値」を、③の式に「x」と「y」を代入しますと上の表の右側の部分に示されているように答えがすべて「１」となり③の式を満たしていました。

そこで、今度は、③と④と⑤の関係から、次のようにおき、

⑤´　1 = x² - 2ｙ² = (x + ｙ√2)(x - ｙ√2)

1² = 1 であることを利用して、平方三角数「１」の場合の解（x,y） = (3,2) を代入し、さらに両辺を「平方」して、次のようにおきました。

⑤´´　1 = 1² = (3 + 2√2)²(3 - 2√2)²

で、これを解いていきますと、

つまり、平方三角数「１」の場合の解（x,y） = (3,2) を⑤´の式に代入し、さらに「平方」したものを計算していくと、

⑤´´　1 = 1² = 17² - 2・12²

となり、

次の平方三角数「３６」に対応する「xの値」（１７）、「yの値」（１２）が得られる、つまり次の平方三角数の解（x,y） = (17,12) を作り出せたんです。

では、次の平方三角数「１２２５」の解（x,y） = (99,70) も同じように求められるのでしょうか？というところまでが、昨日までのお話になります。

それでは、早速、次に進みましょう💛

⑤´　1 = x² - 2ｙ² = (x + ｙ√2)(x - ｙ√2)

の式に、平方三角数「１」の場合の解（x,y） = (3,2) を代入し、先ほどとは違って、今度は1³ = 1 であることを利用して、つまり、両辺を「平方（２乗）」ではなく「３乗」してみます。

⑤´´´　1 = 1³ = (3 + 2√2)³(3 - 2√2)³

そして、これを解いていくのですが、

= (3 + 2√2)(3 + 2√2)(3 + 2√2)×(3 - 2√2)(3 - 2√2)(3 - 2√2)

・・・と、こんな風に計算するのが面倒なので、別の方法を考えます。

~~= (3 + 2√2)(3 + 2√2)(3 + 2√2)×(3 - 2√2)(3 - 2√2)(3 - 2√2)~~

例えば、(a + b)³ というのは、縦が「a+b」、横が「a+b」の正方形の折り紙を、高さ「a+b」に積み上げた立方体の体積を求めることと同じになります。

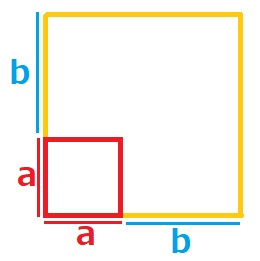
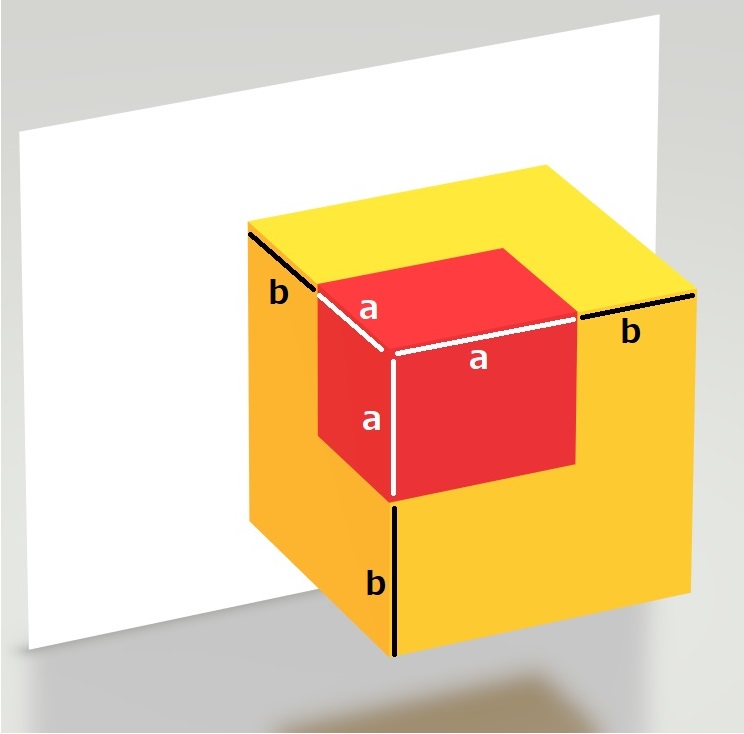
ですから、上の立方体に下のように区切って、左右それぞれの体積を考えますと、

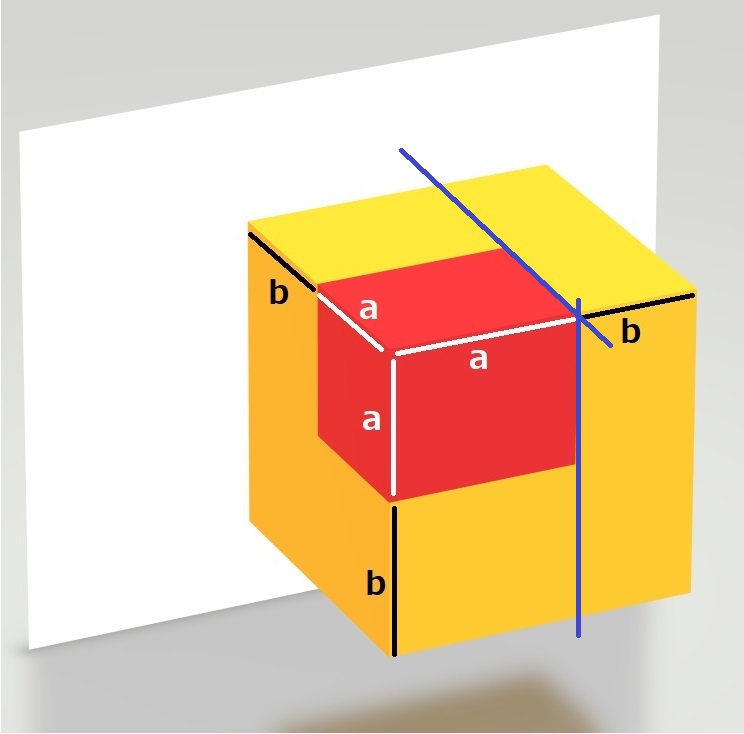
向かって左側が、

a × (a + b)²

向かって右側が、

b × (a + b)²

となりますので、全体の体積は、

(a + b)³ = a × (a + b)² + b × (a + b)²

と表すことができます。これを利用して、

(3 + 2√2)³ = 3 × (3 + 2√2)² + 2√2 × (3 + 2√2)²

= 3 × (9 + 12√2 + 8) + 2√2 × (9 + 12√2 + 8)

= 3 × (17 + 12√2) + 2√2 × (17 + 12√2)

= 51 + 36√2 + 34√2 + 48

= 99 + 70√2

よって、⑤´´´の式から、

⑤´´´　1 = 1³ = (99 + 70√2)(3 - 2√2)³

となります。次に、(a - b)³ というのは、縦が「a-b」、横が「a-b」、高さ「a-b」の立方体の体積を求めることと同じになります。

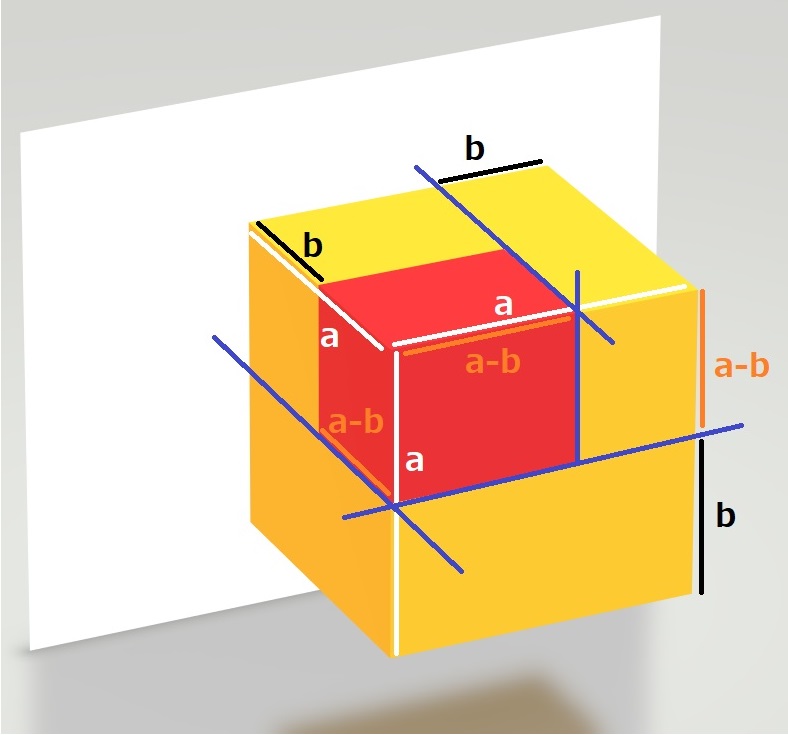
で、さきほどと同じように考えて、

全体の体積　-　底部の体積 - 右側上部の体積 - 奥上部の体積

を式でおきます。すなわち、求める体積は、

a³ - a²b - ab(a - b) - b(a - b)²

と表すことができます。これを利用して、

(3 - 2√2)³ = 3³ - 3²・2√2 - 3・2√2(3 - 2√2) - 2√2(3 - 2√2)²

= 27 - 18√2 - 18√2 + 24 - 2√2(3 - 2√2)²

= 51 - 36√2 - 2√2(3 - 2√2)²

= 51 - 36√2 - 2√2(9 - 12√2 + 8)

= 51 - 36√2 - 2√2(17 - 12√2)

= 51 - 36√2 - 34√2 + 48

= 99 - 70√2

よって、⑤´´´の式から

⑤´´´　1 = 1³ = (99 + 70√2)(99 - 70√2)

整理しますと、つまり、

⑤´´´　1 = 1³ = 99² + 2・70²

となりますので、次の平方三角数「１２２５」の解（x,y） = (99,70) も同じように求められることが分かりました。

さて、考えなければならない問題は、

（問）　三角数の中に平方数になるものは無数に存在するか？

でしたので、このままでは答えとはなりませんので、あと、もう少し考えてみる必要があります。それは、次回以降に書かせて頂きたいと思います。