歴史を見直そうという動きは、すでに世界的な潮流なんです！！

2019-01-08 (Tue)

本日のキーワード　：　歴史修正主義

歴史修正主義（れきししゅうせいしゅぎ、英: Historical revisionism、独: Geschichtsrevisionismus、仏: Révisionnisme）とは、新しく発見されたとされる史料に基づく解釈や、既存の知識を再解釈することにより、歴史を叙述し直すことを主眼とした、歴史学における試みの一つを表す。一般には、伝統的な歴史解釈に対し、別の可能性（仮説）や、可読性（読み方）を提示する試みをいう。

本日の書物　：　『アメリカの「反中」は本気だ！』　宮崎正弘　ビジネス社

戦後の日本人は、正しい歴史を学校で教わって来ませんでした。

そして、現代のメディアもまた、嘘の情報を流し続けています。

私たち日本人は、親日的な立場に立ち、正しく認識し直し、

客観的に情勢を判断する必要があります。

それでは、この書物を見ていきましょう！

『　問題は【華字紙】の【底意地の悪い論調】だろう。

　いまも【おしなべて反日色が濃い】が、それぞれの国の政治情勢が加わり、ときに【中国政府の宣伝を批判するような記事】にお目にかかる。

　あの戦争（【大東亜戦争】）は世界の人々の幸せを踏みにじり、とりわけ【アジア・アフリカ諸国を蹂躙（じゅうりん）】し、【有色人種を奴隷のごとく扱って搾取】してきた【白人国家への日本の挑戦】だった。

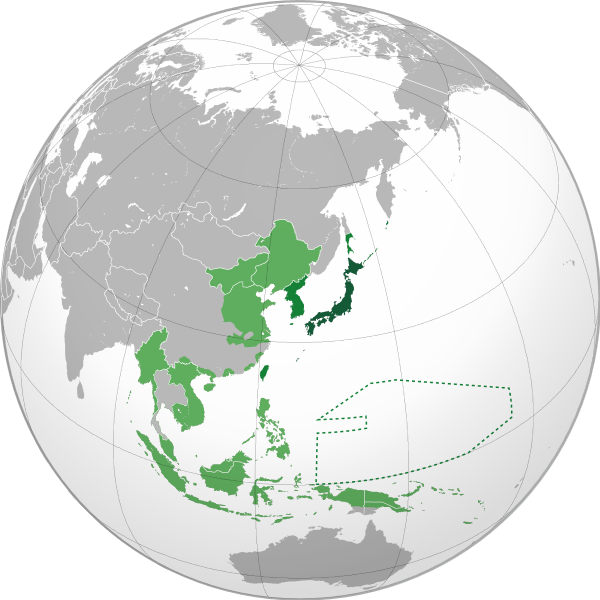
大日本帝国　最大行政統治・軍事勢力圏

「日本がアジアを侵略した」などという【自虐史観】は【東京裁判でＧＨＱが押し付けた改ざん史観】だが、欧米の洗脳にひっかかっている【似非（えせ）知識人】と【朝日新聞】と【左翼】が【共同してでっち上げたもの】だ。

　【大東亜戦争の目的】は【アジアを植民地の桎梏（しっこく）から解放させること】にあった。【この崇高な歴史的意義】が、戦後７０年以上も忘れられてきた。

桎梏（しっこく）

　しかし【アジア諸国】を回って知識人らと話し込むと【華夷秩序にしたがう朝鮮半島の国をのぞき】、おしなべて【日本に感謝している】ことがわかる。

　インドネシア独立戦争も、マレーシアも、ベトナムも残留した【日本兵が対米戦争の戦術を指導】したし、インドの独立戦争は【ともに闘った】事実は厳然としてある。わたしたちは【日本のアジアへの貢献】を正面から【再評価するべきとき】を迎えており、【自虐史観とは永遠に訣別しなければならない】。

　そして【近年、特筆すべきことがアジアで起きている】。それは【日本の評価の見直し】である。

アジアの歴史は、独立後、それぞれが見直しに入ったが、米軍の圧倒的パワーが残存しており、また英字新聞の影響と英米留学帰りの学者ジャーナリストが英米で教わった通りの歴史観で反日を教育し、日本悪玉論がメディアの論調の主流だった。

　中国の反日論調が華字紙に伝わり、それを英語に翻訳するのが中国人ジャーナリストゆえに反日が揺るがぬ歴史観だった。

　それが【近年、なぜ変化したのか】。【各国が自己のアイデンティティーを見直す】という作業のなかで、【独立の先駆者をたたえる】という【歴史の見直し】が始まり、【それぞれの国で、それなりの「国学」が復活】したことと密接な関係がある。』

ガーナ共和国でも歴史の見直しが始まっています

いかがでしょうか？

今回ご紹介させていただく書物は、当ブログでも度々ご紹介させて頂いております、当代随一のチャイナ・ウォッチャーである著者による、優れた「良質なる情報」が詰まった良書となります。ぶっちゃけ、朝日新聞などのサラリーマン記者は、自分の足で「情報」を得るなどといった面倒なことをやらないので、「コピペ」をするか「捏造」するかという二者択一で、やっつけ仕事の記事を日々描き続けるという、とんでもなく愚かで退屈なルーティン・ワークを、何ら疑問視することなくやり遂げることができるそうなのですが（ひょっとしたら、それがご自慢なのかもｗ）、そんな愚者とは違って、お金を出して買う意味がある著者の書物は、幅広く私たち日本人が共有すべきものではないかと考えており、お薦めの書物となります。

さて、みなさんは「ガーナ共和国（the Republic of Ghana）」をご存じでございますでしょうか？

サッカーがお好きであれば、ある程度は御存じでいらっしゃるのではないかと思うのですが。。。

地理的な位置は、御覧のように西アフリカと称される地域に位置していて、

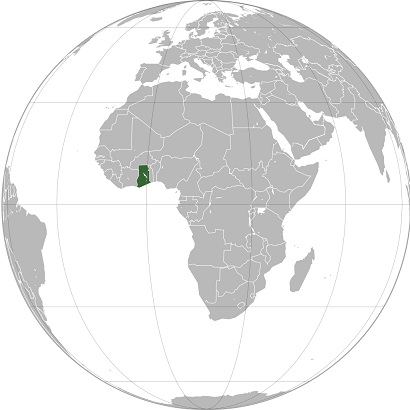
人口は約２９００万人ほどで、私たちの日本の国土の約３分の２の面積の国です。

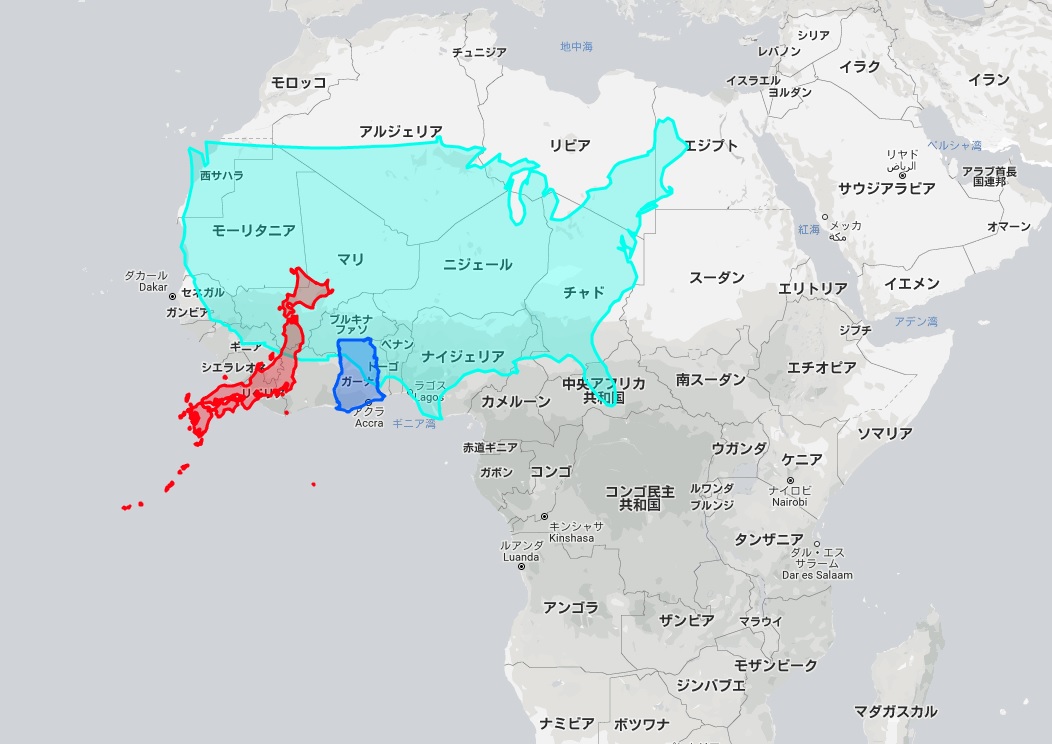
☆The True Size Of ...

本文中にも書かれていましたように、私たちの日本（大日本帝国）が大東亜戦争を戦った目的は、まさにアジアを植民地の桎梏（しっこく）から解放させること、つまり、植民地支配を受け続けたアジアの人々を、それを縛り続けている「手枷足枷（てかせあしかせ）」から「解放」し、人々に「自由」を与えんとすることでした。

それの何がダメだ言うのか、サッパリ分からないのですが、何故か、日本の「左翼リベラル」と呼ばれる「救いようがないバカ」な連中は、それを否定するんです（笑）

例えば、大東亜戦争で私たちの日本は敗戦したわけですが、でも、それは「負けたフリをしているだけ」なのかもしれないわけですが、終戦後に、イギリスから独立した国は５５か国もあり、フランスから独立した国も２９か国あり、ちっぽけなオランダからも２か国が独立しています。

詳しくはこちらをご参照💛
↓
☆（問）　フランスの植民地から独立した国は、いくつあるでしょう？

　

そんなイギリスから搾取され続けていた植民地の中で、独立を果たしたのが「ガーナ共和国」で、それはサハラ以南のアフリカにおいて、史上初めて、現地人が中心となってヨーロッパの宗主国から独立を達成した国家になります。

さきほど、本文中に、植民地から独立を果たした国々が、「自己のアイデンティティーを見直す」という流れが生じていると書かれていましたが、その一つの例が、この「ガーナ共和国」になります。

最近のニュースで、次のような報道がなされていました。

この報道をそのまま鵜呑みにするわけにはいきませんが、当ブログでは、そもそもガンジーには何ら歴史上の価値はないと喝破しておりますので、どうでも良いことになりますが、ここから理解できるのは、「自己のアイデンティティー」の再構築の動きが加速しているのではないか、ということになります。

そんな「ガーナ共和国」と、私たちの日本との関係は、どうなっているのでしょうか？

もちろん、植民地であった国々が「自己のアイデンティティー」の再構築を加速させればするほど、その先には私たち日本人の偉大な先輩方が無視できない存在として浮かび上がってくることになります。これが、いま、世界中で現実に起こっている事象になります💛

それでは、「ガーナ共和国」の場合は、どうなのでしょうか？　

私たちの日本が誇る天才・野口英世が、５１歳という若さで永眠した地、それがイギリスの植民地支配を受けていた頃の「ガーナ共和国」です。

野口英世

本日の課題　：　（問）　三角数の中に平方数になるものは無数に存在するか？

さて、ここからは昨日の続きになります。

昨年の暮れから、次の問題について考えているところになります。

（問）　三角数の中に平方数になるものは無数に存在するか？

平方数の例

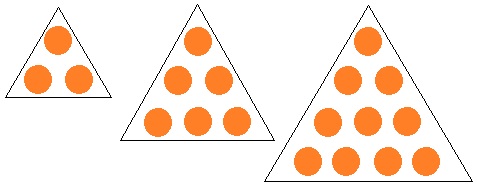
三角数の例

つまり、「平方三角数」が無限に存在するのかどうか、ということを考えているところです。

そして、平方数の式を「ｎ」を使って、三角数の式を「m」を使って、次の式を得ました。

①　2×(2n)² = (2m + 1)² -1

ここで、「平方三角数」となる数を求めるために、

②　y = 2n、x = 2m + 1

と置き換えました。

①に②を代入して得られた式が、次のものになります。

③　x² - 2ｙ² = 1

さらに、そこから得られた式が、次のものになります。

④　(x + ｙ√2)(x - ｙ√2) = 1

昨日のところでは、求めるべき「平方三角数」は、③または④の方程式を満たす解（x,y）であるはずと考え、それを探し出すために、、

②　y = 2n、x = 2m + 1

から、

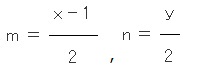
とおき、「x」と「y」のそれぞれに、１から１００までの数字を順に入れて、「m」と「n」を求めていき、という風に、試行錯誤を試みました。

でも、トンデモナク面倒ですので、違う方法を考えたい、そう思っているところです。どのように、考えれば良いのでしょうか？

私たちは、いま、次の式を理解しています。

③　x² - 2ｙ² = 1

もちろん、それを変形しただけの、

④　(x + ｙ√2)(x - ｙ√2) = 1

も理解しています。

③の右辺と④の右辺は同じですから、当然、次のように表すことができます。

⑤　x² - 2ｙ² = (x + ｙ√2)(x - ｙ√2)

昨日のところで、実際に手間をかけて調べてみたところ、３つの平方三角数、つまり「１」と「３６」と「１２２５」を発見することができたのですが、

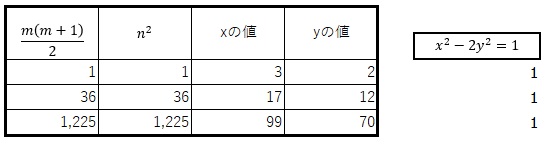
上の表は、昨日のところでも書かせて頂いたものですが、左から「三角数」、「平方数」、それらに対応する「xの値」、「yの値」となっているのですが、「三角数」であり、かつ「平方数」である「平方三角数」に対応する「xの値」、「yの値」と言い換えることができます。そして、それが正しいかどうかを③の式に「x」と「y」を代入して確認しているのが右側の部分になります。

では、本日は⑤の式を活用してみたいと思います。

⑤　x² - 2ｙ² = (x + ｙ√2)(x - ｙ√2)

③と④と⑤の関係から、

⑤´　1 = x² - 2ｙ² = (x + ｙ√2)(x - ｙ√2)

となることは自明です。

ここで、平方三角数「１」の場合の解（x,y） = (3,2) を⑤´の式に代入してみますと、

⑤´　1 = 3² - 2・2² = (3 + 2√2)(3 - 2√2)

少し整理致しまして、

⑤´　1 = 1 = (3 + 2√2)(3 - 2√2)

さて、ここで、

1² = 1

であることを利用して、両辺を「平方」してみます。つまり、

⑤´´　1 = 1² = (3 + 2√2)²(3 - 2√2)²

となりますので、さらに進めますと。。。

⑤´´　1 = 1² = (3 + 2√2)(3 + 2√2)×(3 - 2√2)(3 - 2√2)

= ｛3・3 + 3・2√2 + 3・2√2 + 2√2・2√2｝×｛3・3 + 3・(-2√2) + 3・(-2√2) + (-2√2) ・ (- 2√2)｝

= ｛9 + 3・2√2+ 3・2√2 + 2√2・2√2｝×｛9 + 3・(-2√2) + 3・(-2√2) + (-2√2) ・ (- 2√2)｝

= (9 + 6・2√2 + 2√2・2√2)×｛9 -6・2√2 + (-2√2) ・ (- 2√2)｝

= (9 + 12√2 + 2√2・2√2)×｛9 -12√2 + (-2√2) ・ (- 2√2)｝

= (9 + 12√2 + 2・2・√2・√2)×(9 -12√2 + (-2)・(-2)・√2・√2)

= (9 + 12√2 + 2・2・2)×(9 -12√2 + (-2)・(-2)・2)

= (9 + 12√2 + 8)×(9 -12√2 + 8)

= (17 + 12√2)×(17 -12√2)

= 17²+ 17・12√2 - 17・12√2 + ｛12√2 × (-12√2)｝

= 17² + ｛12√2 × (-12√2)｝

= 17² - (12√2 × 12√2)

= 17² - (12² × √2 × √2)

= 17² - 2・12²

つまり、平方三角数「１」の場合の解（x,y） = (3,2) を⑤´の式に代入し、さらに「平方」すると、

⑤´´　1 = 1² = 17² - 2・12²

となるわけです。ここで、何かお気付きになられませんでしょうか？

平方三角数「１」に対応する「xの値」（３）、「yの値」（２）を、⑤´の式に代入し、さらに「平方」すると、なんと、次の平方三角数「３６」に対応する「xの値」（１７）、「yの値」（１２）が得られている、つまり次の平方三角数の解（x,y） = (17,12) を作り出せたのです。

それでは、次の平方三角数「１２２５」の解（x,y） = (99,70) も同じように求められるのでしょうか？

ということで、本日はここまでとさせて頂きます。