2018-11-26 (Mon)

『金魚』 リチャード・E・ミラー
金魚鉢(きんぎょばち)とは、魚(主に金魚)の観賞を目的としたガラス製の鉢。

フィリップ・ド・ラースロー画
戦後の日本人は、正しい歴史を学校で教わって来ませんでした。
そして、現代のメディアもまた、嘘の情報を流し続けています。
私たち日本人は、親日的な立場に立ち、正しく認識し直し、
客観的に情勢を判断する必要があります。
それでは、この書物を見ていきましょう!
『 ものごとを【長い目で見る人】がいます。反対に、【短い目でしか見られない人】もいる。

【新聞記者】の【大半は後者】です。

いつも【その場限りの解説記事】を書き、それを書き上げると、【他のメディアはどう書いているか】が気になって、自分が今書いたものが【多数派の中に入っているかどうかと周りを見回します】。そして、【入っていれば一安心】。

誰でも新聞社に入ったときは、読者をアッといわせるようなものを書きたいと張り切っていますが、先輩に原稿を手直しされたり、上司からうるさく言われたりしているうちに、いつしか最初から【上司に気に入られる記事を書く】ようになってしまいます。日本語でいうならば【「手なれたベテラン」】、英語でいえば【「シーズンド・プレスマン」(手なれた新聞記者)】になります。

☆東京新聞・望月衣塑子氏「野党が…野党が…」→ 菅官房長官「野党の事に私が答える立場にありません」
新聞や雑誌を意味する【「ジャーナル」】という言葉はそもそも【「ヤヌス」】という双面神(そうめんしん)に由来しているという説があります。

顔が2つあるヤヌス神は【「昨日」と「明日」の境界】に立ち、その【両方を見ている】のです。もしその説にのっとるならば、【ジャーナリズム】とは本来、【その場限りの報道をするのではなく】、【「昨日」と「明日」を見据えた発信をすべき】です。ところが、【いまの新聞記者たち】はそうした【「ジャーナル」の原義を忘れてしまった】ため、【近視眼に陥っています】。

学生時代、政治学の教授から
「【“金魚鉢の法則”】というのを知っているか?」
と訊かれたことがあります。

「知りません。教えてください」
と答えると、
「鉢に入れられた金魚は右へ行ってガラスにぶつかり、左へ行ってまたぶつかる。そんなことをしているうちに、やがて金魚鉢の寸法を覚えて、もうぶつからなくなる。身をもって会得したことだから、それはそれでいいのだが、もう少し大きい金魚鉢に入れても、金魚はやっぱり中心部ばかりクルクル回っているんだね。これは【“サラリーマンの法則”】と呼んでもいいんじゃないかな」
と。そして、教授はニヤッと笑いました。

【終身雇用に安住した記者】にとって【金魚鉢】は【自分が属する新聞社】ですが、いまは若者たちの【新聞離れが進んで、朝日も読売も毎日も…発行部数をどんどん落としています】。…

これではもう【「新聞崩壊」】と呼んでもさしつかえないでしょう。じっさい、【日本の大新聞】は【ステレオ・タイプの論ばかり書いている】ために、【すっかり読者から飽きられ、見放されています】。』

いかがでしょうか?
今回ご紹介させていただく書物は、これまでにも何冊かご紹介させて頂いております著者による書物になりますが、大変失礼な言い方かもしれませんが、優れた経験と見識を持った「長老」のご意見のような、非常に参考になる、その自由な「考え方」や「発想」について、学べる点が非常に多い良書となります。

さて、本文中の「金魚鉢の法則」については、多くの方々が納得できることではないでしょうか?

本文中では、「金魚 = サラリーマン」、「金魚鉢 = 所属会社」という関係になっていますが、これは別にいくらでも言い換えが可能で、「金魚 = 官僚」ですし、「金魚鉢 = 所属省庁」です。他にも、いくらでも別の表現ができますね💛

それでは、そんな「金魚鉢の法則」の、どこがダメなのでしょうか?

それをご理解頂くために、次の「数学の問題」(中学生レベル)を考えてみましょう。

(問) 次の平行四辺形ABCDで、対角線ACとBDの交点をOとする。また、辺BCの中点をEとし、AEとBDの交点をFとする。次の問いに答えなさい。
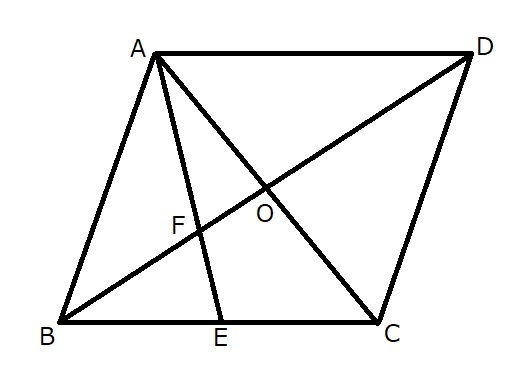
(1) DF:BFを求めなさい。

さて、如何でございますでしょうか?
解き方、つまり、答えの求め方というものは、いくつも考えられますが、「より単純で分かりやすく」、「誰にでも理解しやすい」、というやり方の方が、何かと面倒くさがり屋の当ブログ(笑)にとっては、より好ましいのではないかと、勝手に思っているわけですが、ご批判は承知の上で考えてみたいと思います。

まず、平行四辺形の定義は、
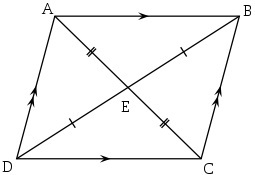
(ⅰ) 対辺の長さが等しい(対辺は2組あるが、いずれもこの性質を満たす)。
(ⅱ) 対角の大きさが等しい(対角は2組あるが、いずれもこの性質を満たす)。
(ⅲ) 対角線が他の対角線の中点を通る(対角線は2本あるが、いずれもこの性質を満たす)。
となります。

ですので、(ⅲ)から、
DO:BO=1:1
ということが分かっています。また、(ⅰ)から、
AD = BC
ということが分かっています。
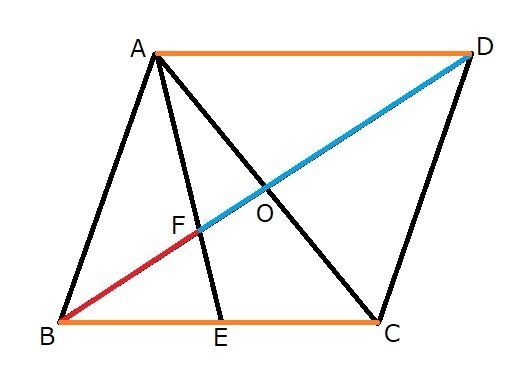
さて、どのように考えれば良いでしょうか?

ここで、ご提案ですが、「金魚鉢」、

つまり、この問題に描かれている「平行四辺形」を、突き破ってみても良いのではないでしょうか?

例えば、こんな風に。
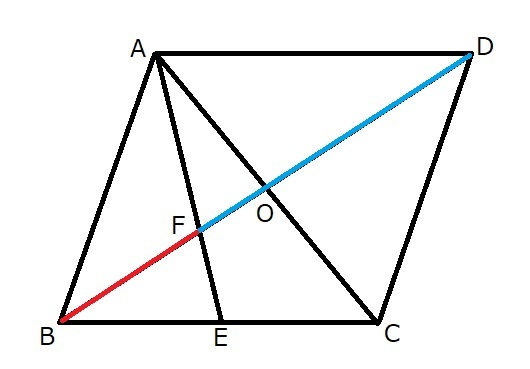
まず、点Eから点Oを通って辺ADまで線を描きますと、辺ADの中点が示されます。
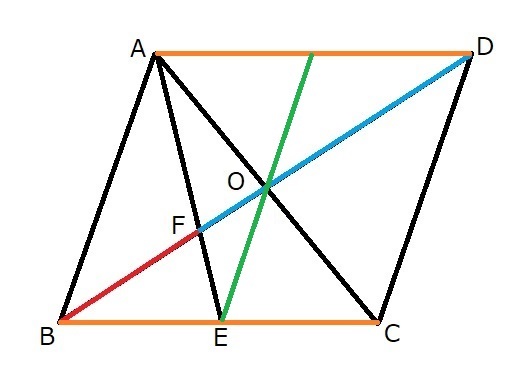
そして、今度は、その辺ADの中点と点Cを通る線分を描きます。これは線分AEと平行になります。
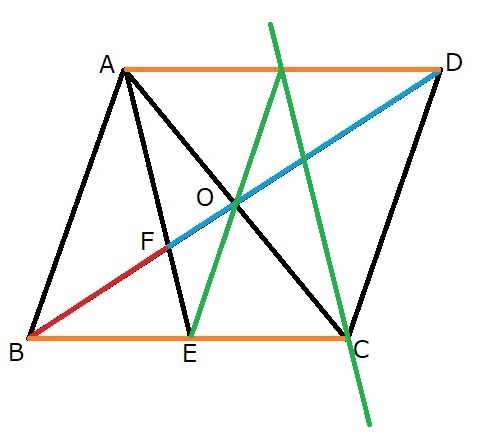
で、調子に乗って、元の平行四辺形をもっと串刺しにしてしまうと。。。
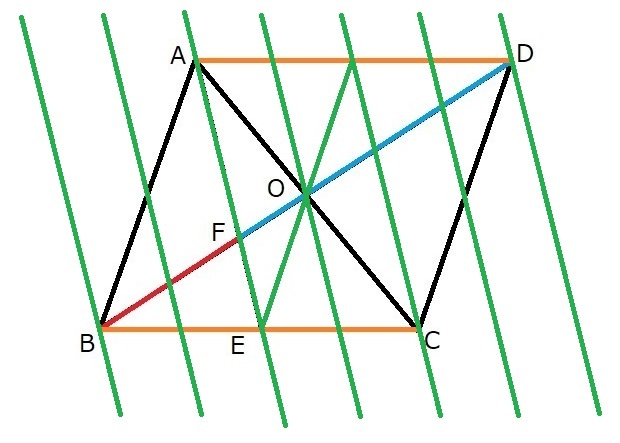
で、問題をもう一度確認してみますと、
(1) DF:BFを求めなさい。
でしたので、
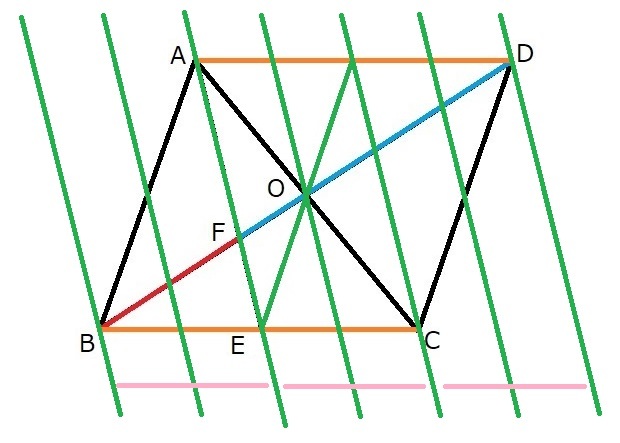
答えは、
2:1
となります。同じように、次の問題も簡単に解けます。

(2) FO:BDを求めなさい。

で、次の2つの問題も、チャレンジしてみてください。

(3)三角形AFOと平行四辺形ABCDの面積の比を求めなさい。
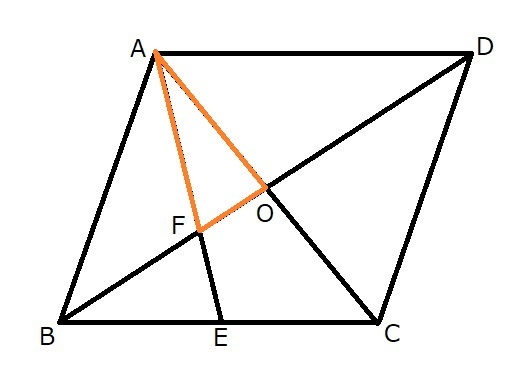
(4)三角形AODと三角形BEFの面積の比を求めなさい。
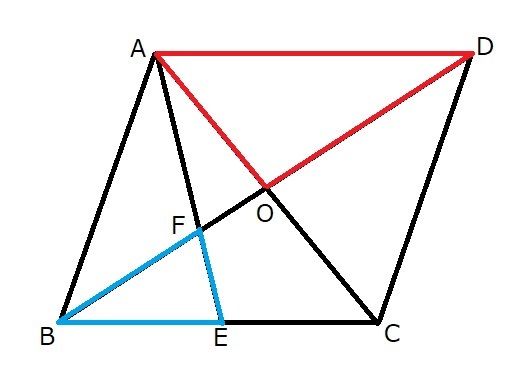

ぜひ、「金魚鉢」を突き破って、自由な発想で解き明かしてみてください。複雑な計算は不要な中学生レベルの問題ですので💛
続きは次回に♥
ランキング参加中で~す^^ ポチっとお願いします♥
↓↓↓↓↓↓↓
にほんブログ村

人気ブログランキング

- 関連記事
-
- 歴史は女性がつくってきたものです。 (2019/01/15)
- 「男性」や「世の中」や「日本国」を良くするための「必要条件」 (2019/01/14)
- LGBTではなく、「LGBS」と表現すれば、簡単に理解できること (2019/01/13)
- 新自由主義 = グローバリズム = 中華人民共和国 (2018/11/30)
- 「汚職」に手を貸す朝日新聞と立憲民主党 (2018/11/29)
- 「岩盤規制」と「既得権益」と「社会主義」 (2018/11/28)
- 【生物学上の分類(?!)】 日本人=「ヒト」、朝鮮類人猿=「コリラ(Korilla)」、支那類人猿=「チナパンジー(Chinapanzee)」 (2018/11/27)
- 朝日新聞と「金魚鉢の法則」 (2018/11/26)
- 他人から借金する必要がないということを、誰もお金を貸してくれないこと、と思い込んでしまう人 (2018/09/03)
- 「権力は腐敗する」のだそうです(笑) ~ 腐敗することは、すべて「悪」なのでしょうか? (2018/09/02)
- パンドラの箱に残されたものって何? (2018/09/01)
- 三歳児神話を否定するのは、「日本だけ」なんです! (2018/08/27)
- 日本人の常識的な感覚とは違う「一群の方たち」 (2018/08/26)
- 左翼リベラルの「全体主義(ファシズム)」と、それに利用される道具に過ぎない「LGBT」 ~ 杉田水脈さん、頑張って💛 (2018/08/25)
- 「見える河川」と「見えない河川」 (2018/07/19)
