日本人は「数」をどのように表現していたのでしょうか？

2018-09-04 (Tue)

数字（すうじ、英: numeral）とは数（数値、数量、英: number）を表現するための記号（英: figure, 英: digit）および文字（英: character, 英: letter）である。

ただし日本では、数字は数自身と混同されることが多いが、これによって問題を生じることもある。

戦後の日本人は、正しい歴史を学校で教わって来ませんでした。

そして、現代のメディアもまた、嘘の情報を流し続けています。

私たち日本人は、親日的な立場に立ち、正しく認識し直し、

客観的に情勢を判断する必要があります。

それでは、この書物を見ていきましょう！

『　「数学とは何か」「数学にとって身体とは何か」を問う私の探求の原点には、【岡潔】（１９０１～１９７８）という数学者との出会いがある。

岡潔

　大学に入って間もない頃のことだ。私はたまたま通りがかりの古書店で、【『日本のこころ』】という本に巡り合った。それは【岡潔の代表的エッセイを編んだ選集】で、当時すでに絶版の文庫版だったが、タイトルといい、本の体裁といい、とても【数学の本には見えなかった】。難解そうな数学書の並びの中で、ひときわ不思議な魅力を放っていた。

　

　その頃私は、【文系の学部に所属】していて、まさか自分が【数学に夢中になる】とは思ってもいない。だが、振り返ればあの日に私は後戻りのできない【数学の道】への最初の一歩を、確かに踏み出していたのである。

　大学には数学好きの友達がいて、いつも私にいろいろなことを教えてくれた。中でも彼が聞かせてくれる、数学者の奇抜で型破りなエピソードは、格別に面白かった。

　素数の研究に夢中になるあまり、服を着るのを忘れたまま登校してしまった先生の話とか、普段の授業があまりにも完璧なので、授業中に一瞬行き詰まっただけで「あの先生が止まったぞ！」と教室全体が沸いた話とか、にわかには信じがたいような、愉快な話がたくさんあった。

　アルキメデスやオイラーやガウスのような、過去の偉大な数学者の名前は多少は知っていたけれど、グロタンディークやベレルマンやウィッテン、ましてや日本の大学にいる同時代の数学者についてはほとんど何も知らなかった私にとって、刺激的な話ばかりだった。そんな彼のおかげだろうか。【岡潔】という名前だけは、どこかで聞いた覚えがあったのである。

　私はその日手にした『日本のこころ』を、夢中になって読んだ。そこには【今まで知らなかった広大な世界】が開けているように思われた。それでいて、【どこか懐かしい】ような、【前からよく知っている世界】のような、【不思議な感覚】に包まれた。そこには狭い意味での数学を超えて、【生きること】、あるいは【「わかる」こと】について、【全身の実感のこもった言葉】が並んでいたのだ。

　【岡潔】によれば、【数学の中心にあるのは「情緒」】だという。【計算や論理は数学の本体ではなく】て、肝心なことは、【五感で触れることのできない数学的対象に、関心を集め続けてやめないこと】だという。【自他の別】も、【時空の枠】すらをも【超えて】、【大きな心で数学に没頭】しているうちに、【「内外二重の窓がともに開け放たれることになって、『清冷の外気』が室内にはいる」】のだと、彼は独特の表現で、数学の喜びを描写する。

　私は高校までバスケットボールに夢中だった。勝ち負けよりも、【無心で没頭】しているときに、【試合の「流れ」ともに一体化】してしまう感覚が好きだった。バスケに「真実」というものがあるとすれば、それは正しい論理を身につけることでも、戦術をたくさん覚えることでもなく、【ただバスケという行為に没入】しきって【「体得」するほかないもの】だと感じていた。

　【岡潔の言葉】を読んでいると、なぜか不思議と、バスケに捧げた日々を思い出した。この人にとって数学は、全心身を挙げた行為なのだと思った。頭で理屈を捏（こ）ねることでも、小手先の計算を振り回すことでもなく、生命を集注して数学的思考の「流れ」になりきることに、この人は無上の喜びを感じていることが伝わってきた。

　私は、【岡潔】のことをもっと知りたいと思った。彼が見つめる先に、【自分が本当に知りたい何かがある】のではないかとも思った。簡単に言えば、【「この人の言葉は信用できる」と直観したのだ】。

　【数学と身体】を巡る私の旅も、ここから始まったのである。【岡潔の語る数学】は、【それまでに私が知っていたものとはまったく違った】。そこには、【生きた身体の響き】があった。【「数学」と「身体」】－－とてつもなくかけ離れて見える【この二つの世界】が、実はどこかで【深く交わっている】のではないか。その交わる場所を、この目で確かめたいと思った。ならば、数学の道へ分け入るしかない。私は、数学を学ぶ決心をした。』

いかがでしょうか？

今回ご紹介させていただく書物は、一見すると無関係のように思ってしまいがちな、「数学」と「身体」について、古代から現代に至るまでの、両者の関わり方やその関係性の変化について、数学の発展の歴史を解説するとともに、著者ご自身が偉大な数学者である岡潔とアラン・チューリングの影響を受け、数学への道を歩み始めることになった心情を綴った書物になります。

さて、本書の冒頭部分でご紹介されているお話に、心理学でいうところの「スービタイゼーション（subitization）」について書かれているのですが、これは人間の「数」の認知能力のことで、少数のものであれば即座に把握できる（提示された対象の数を瞬時に知見する）能力が、もともと備わっているというお話になります。普通一般的には３つぐらいまでで、人間の能力の限界は６つだと考えられています。

物は試し、ということで、実際にチャレンジしてみましょう💛

次の動画（↓）に表示されるものの「数」を瞬時に答えてみてください。

如何でしょうか？

それでは、もう一つお試しください💛

さて、如何でしたでしょうか？

単純なものですが、なかなか難しいところもあって、実感できたのではないでしょうか？

古代インドで用いられた「ブラーフミー数字」は、紀元前３世紀以前のものと考えられていますが、現代のインド数字やアラビア数字の元となったものです。

漢数字の「一」、「二」、「三」は、このブラーフミー数字とそっくりですね💛

ところで、先ほど、人間が瞬時に「数」を把握できるのは普通一般的には３つぐらいまで、と書かせて頂きましたが、ブラーフミー数字も“４”以降は、“１～３”までの表記とは少し違っていると感じられませんでしょうか？

例えば、ローマ数字も、“１・２・３”は“Ⅰ・Ⅱ・Ⅲ”と表していますが、“４・５・６・７・８・９・１０”になると、“Ⅳ・Ⅴ・Ⅵ・Ⅶ・Ⅷ・Ⅸ・Ⅹ”という表し方になり、覚えるのが大変です。

漢数字も、“一、二、三”に続くのが、“四、五、六、七、八、九、十”で、“四”以降の表記がそれ以前の“一から三”までとは変わっています。

これらは、「スービタイゼーション（subitization）」と何か関係があるのかもしれませんね💛

ちなみに、現代の私たち日本人も馴染みが深い「アラビア数字」の“１・２・３・４・５・６・７・８・９”は、次のような法則で成立しています。“ゼロ”は「・」の無い「０」になります。

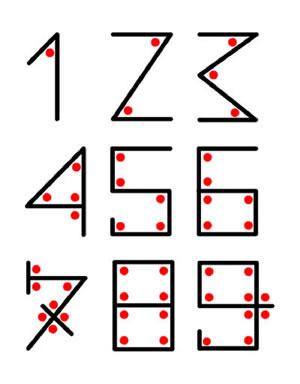
ところで、私たち日本人のもともとの言葉、「和語（やまとことば）」では、「数」をどのように呼んでいたのでしょうか？

まず、“１”は「ひと」、そして、“２”は「ふた」です。

「ひと（hito）」と「ふた（huta）」は母音交替（ぼいんこうたい）といって、母音が変化することで別の単語に変化（派生）する特徴が見られ、両者は倍数の関係になっています。

これと同様に、“３”は「み」、“６”は「む」で、「み（mi）」と「む（mu）」も母音交替による倍数の関係にあることが分かります。

もちろん、“４”は「よ」で、“８”は「や」ですから、「よ（yo）」と「や（ya）」も母音交替による倍数の関係にあります。

では、“５”とか“７”とか“９”も同じなのでしょうか？

実は、違います。

ここまで、「和語（やまとことば）」で「数」をどのように呼んでいたのかということで、“１、２、３、４、６、８”について書かせて頂きましたが、「数そのもの」ではなく「数量」として言い表す場合には、「助数詞のツ」を伴った語形、つまり、「ひとつ」、「ふたつ」、「みつ」、「よつ」、「むつ」、「やつ」となるのですが、“１０”になると、その区別がなされなくなります。

ですから、“１～９”までの扱いと“１０～”の扱いは異なっています。そこで、さきほどの“５”とか“７”とか“９”については、母音交替の倍数関係にすると扱いの異なった“１０”を超えてしまいますので、不可能だったのではないでしょうか、と思えるのですが、果たしてどうなのでしょうか。。。

ところで、「助数詞のツ」を伴わない「ひと」の意味には、「不可分」や「単一」の意味があります。「一つ」「一度」の意はもちろん、「ほんの少し」「ちょっと」とか「同じ・同一の」とか「全部・全体」という意味や、「いっぱい・大量」や「第一・一番」といった意味も表しています。

一方で、「助数詞のツ」を伴わない「ふた」の意味には、二つ揃って一対であるものの揃った状態である両方・双方の意味と、単一ではなく異なっている、別々のという意味があります。

そして、「助数詞のツ」を伴わない「よ（四）」ですが、これは「や（八）」も同様になりますが、無限を意味する「いや（弥）」と同根で、古代において、神話や伝説に特別な「数」として選ばれているものです。

明治天皇の御製「よもの海」、そしてそれを昭和天皇が御前会議において一部言葉を置き替えてお詠みになられたことでも知られるところですね。

詳しくはこちらをご参照💛
↓
☆四方の海みな同胞と思ふ世になどあだ波の立ちさわぐらむ　～　昭和天皇